Существует несколько методов, позволяющих получить решение системы n линейных уравнений с n неизвестными приближенно, с заданной точностью.
Способы решения систем линейных уравнений делятся на две группы:
1) точные методы, представляющие собой конечные алгоритмы для вычисления корней системы (решение систем с помощью обратной матрицы, правило Крамера, метод Гаусса и др.),
2) итерационные методы, позволяющие получить решение системы с заданной точностью путем сходящихся итерационных процессов (метод итерации, метод Зейделя и др.).
Вследствие неизбежных округлений результаты даже точных методов являются приближенными. При использовании итерационных методов, сверх того, добавляется погрешность метода.
Эффективное применение итерационных методов существенно зависит от удачного выбора начального приближения и быстроты сходимости процесса.
Метод Гаусса
1. Схема единственного деления. Рассмотрим сначала простейший вариант метода Гаусса, называемый схемой единственного деления.
Прямой ход состоит из n - 1 шагов исключения.
1-й шаг. Целью этого шага является исключение неизвестного x1 из уравнений с номерами i = 2, 3, n. Предположим, что коэффициент a11 ≠ 0. Будем называть его главным элементом 1-го шага.
Найдем величины
называемые множителями 1-го шага. Вычтем последовательно из второго,
третьего, …, n-го уравнений системы первое уравнение, умноженное соответственно на q21, q31, …, qn1. Это позволит обратить в нуль коэффициенты при x1 во всех уравнениях, кроме первого. В результате получим эквивалентную систему
в которой 
вычисляются по формулам
2-й шаг. Целью этого шага является исключение неизвестного х2 из уравнений с номерами i = 3, 4, n. Пусть a22(1) ≠ 0, где a22(1) - коэффициент, называемый главным (или ведущим) элементом 2-го шага. Вычислим множители 2-го шага
и вычтем последовательно из третьего, четвертого,..., n-го уравнения системы второе уравнение, умноженное соответственно на q32, q42, …, qm2. В результате получим систему
Здесь коэффициенты 
вычисляются по формулам
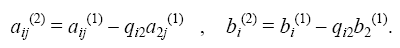
Аналогично проводятся остальные шаги. Опишем очередной k-й шаг.
к-й шаг. В предположении, что главный (ведущий) элемент k-го шага akk(k-1) отличен от нуля, вычислим множители k-го шага
и вычтем последовательно из (k + 1)-го, …, n-го уравнений полученной на предыдущем шаге системы k-e уравнение, умноженное соответственно на 
После (n - 1)-го шага исключения получим систему уравнений
матрица 
которой является верхней треугольной. На этом вычисления прямого хода заканчиваются.
Обратный ход. Из последнего уравнения системы находим xn. Подставляя найденное значение xn в предпоследнее уравнение, получим xn-1. Осуществляя обратную подстановку, далее последовательно находим xn-1, xn-2,., x1. Вычисления неизвестных здесь проводятся по формулам
Необходимость выбора главных элементов. Заметим, что вычисление множителей, а также обратная подстановка требуют деления на главные элементы akk(k-1). Поэтому, если один из главных элементов оказывается равным нулю, то схема единственного деления не может быть реализована. Здравый смысл подсказывает, что и в ситуации, когда все главные элементы отличны от нуля, но среди них есть близкие к нулю, возможен неконтролируемый рост погрешности.
Метод Гаусса с выбором главного элемента по всей матрице (схема полного выбора).
В этой схеме допускается нарушение естественного порядка исключения неизвестных.
На 1-м шаге метода среди элементов aiJ определяют максимальный по модулю элемент 
Первое уравнение системы и уравнение с номером i1 меняют местами. Далее стандартным образом производят исключение неизвестного 
из всех уравнений, кроме первого.
На k-м шаге метода среди коэффициентов 
при неизвестных в уравнениях системы с номерами i = k,., n выбирают максимальный по модулю коэффициент 
Затем k-е уравнение и уравнение, содержащее найденный коэффициент, меняют местами и исключают неизвестное 
из уравнений с номерами i = k + 1,., n.
На этапе обратного хода неизвестные вычисляют в следующем порядке:
Пример. Решить систему методом Гаусса с выбором главного элемента:
Решение системы удобно оформить в виде таблицы
Используя выделенные строки, получим треугольную систему для определения неизвестных
Откуда последовательно находим 
Задания: выполнить задание 4 ИДЗ№1.
