Занятие № 8. Метод итераций для систем уравнений

Цель - ознакомить студентов с методом итераций решения систем линейных алгебраических уравнений.

Рассмотрим систему линейных алгебраических уравнений (СЛАУ):

a₁₁ x₁ + a₁₂ x₂ + … + a_1n x_n = b₁

a₂₁ x₁ + a₂₂ x₂ + … + a₂₁ x_n = b₂

……………………………………..

a_n1 x₁ + a_n1 x₂ +… + a_nn x_n = b_n,

или в векторно-матричном виде:

Ax = B, (1)

где

А = , B= , x=

Итерационные методы решения СЛАУ используются для решения СЛАУ большой размерности с разреженными матрицами, а также для уточнения решения СЛАУ, полученного с помощью прямого метода. Формулировка и применение итерационных методов требует определенных знаний и определенного опыта. Выбор эффективного итерационного метода решения конкретной задачи существенно зависит от ее характерных свойств и от архитектуры вычислительной машины, на которой будет решаться задача. Поэтому никаких общих правил выбора наилучшего итерационного метода решения не существует. Метод простой итерации приведен здесь как иллюстрация действия механизма вычисления решения на основе итерационной процедуры.

Суть метода состоит в следующем. От системы уравнений вида (1) переходят к системе уравнений

x=Dх + С (2)

Например, от системы уравнений

а₁₁х₁+а₁₂х₂+а₁₃х₃=в₁

а₂₁х₁+ а₂₂х₂+а₂₃х₃=в₂ (3)

а₃₁х₁+а₃₂х₂+а₃₃х₃=в₃

можно перейти к виду (2), выразив из первого уравнения х₁, из второго - х₂, из третьего - х₃:

х₁= - а₁₂/а₁₁х₂ - а₁₃/а₁₁х₃+в₁/а₁₁

х₂= - а₂₁/а₂₂х₁ - а₂₃/а₂₂х₃+в₂/а₂₂ (4)

х₃= - а₃₁/а₃₃х₁ - а₃₂/а₃₃х₂+ в₃/а₃₃

Приведение исходной системы уравнений в виду (2) можно осуществить различными способами. Например, в СЛАУ (3) из первого уравнения можно выразить х₂, из второго - х₁, из третьего - х₃ и, переставив уравнения для сохранения порядка следования переменных в векторе решения х, снова прийти к виду (2). Естественно, что матрица D и вектор с будут уже иными. Возможны и другие способы преобразования исходных уравнений.

После преобразования (1) к виду (2) назначается нулевое приближение решения х ^(0):

х₁ ⁽⁰⁾

х ⁽⁰⁾ = х₂ ⁽⁰⁾

х₃ ^(0).

Если приблизительно известны значения х_i вектора решения х, то они выбираются в качестве нулевого приближения, если нет, то в качестве вектора х ⁽⁰⁾ выбирается любой вектор, например х ⁽⁰⁾ =О.

Первый шаг итерационного процесса состоит в вычислении приближения х⁽¹⁾:

х ⁽¹⁾ = Dx ⁽⁰⁾ +С.

Например, назначив х ⁽⁰⁾ и подставив его в систему уравнений (4), получим:

х₁ ⁽¹⁾ = - а₁₂/а₁₁х ^{(0) -} а₁₃/а₁₁х₃ ⁽⁰⁾ +в₁/а₁₁

х₂ ⁽¹⁾ = - а₂₁/а₂₂х₁ ^{(0) -} а₂₃/а₂₂х₃ ⁽⁰⁾ +в₂/а₂₂

х₃ ⁽¹⁾ = - а₃₁/а₃₃х₁ ^{(0) -} а₃₂/а₃₃х₂ ⁽⁰⁾ +в₃/а_33.

Далее вычисляем:

х ⁽²⁾ = Dx ⁽¹⁾ +C

х ^(к) =Dх ^(к-1) +С

и т.д.

Достаточное условие сходимости метода итерации заключается в следующем, если норма матрицы D (обозначается ║D║) меньше 1, то система уравнений (2) имеет единственное решение х^* и итерации сходятся к этому решению со скоростью геометрической прогрессии. Иными словами, если

║D║<1, (5)

то

= 0

и выполняется тождество

х^*=Dх^*+С.

В качестве нормы матрицы D используются нормы ║D║₁ или ║D║_∞:

║D║₁ = ,

║D║_∞= |.

Аналогично вводятся нормы вектора х:

║х║₁ =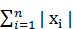

║х║_∞= |x_i|.

Из условия сходимости (5) ясно, что не всякое преобразование исходной системы к виду (2) позволит получить решение уравнения на основе итерационного процесса, а только такое, которое обеспечит выполнение условия ║D║<1. Важно иметь в виду, что при выполнении этого условия итерационный процесс сходится для любого начального приближения х ⁽⁰⁾ и выбор х ⁽⁰⁾ =O диктуется просто соображениями удобства назначения х ^(0).

Условие (5) выполняется, если модули диагональных коэффициентов для каждого уравнения системы больше суммы модулей недиагональных коэффициентов, т. е.

Если задана допустимая погрешность вычислений Δ, то для оценки погрешности к - го приближения широко используется следующее неравенство:

║х ^{(к) -} х*║≤║D║ ∕ (1-║D║) •║х ^(к) - х ^(к-1) ║<Δ (6)

Из этого неравенства следует критерий окончания итерационного процесса

║х ^{(к) -} х ^(к-1) ║ < (1-║ D║) •∆ ∕ ║D║ (7)

Каждый раз при вычислении очередного приближения х ^(k) проверяется выполнение неравенства (7).

Выполнение неравенства (7) означает выполнение неравенства

║х ^(к) - х^*║ < ∆

и, следовательно, прекращение итерационного процесса.

Метод Зейделя.

Метод Зейделя представляет собой некоторую модификацию метода итераций. Основная его идея заключается в том, что при вычислении (k + 1)-го приближения неизвестной x_i учитываются уже вычисленные ранее (k + 1)-е приближения неизвестных x ₁, x ₂, …, x_{i - 1}.

Пусть для системы (1) получена эквивалентная система

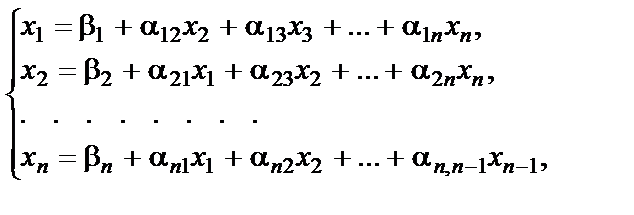
Выберем произвольно начальные приближения корней . Далее, предполагая, что k -ые приближения корней известны, согласно Зейделю будем строить (k + 1)-е приближения корней по формулам:

Метод прогонки.

Метод прогонки является модификацией метода Гаусса для частного случая разреженных систем - системы уравнений с трёхдиагональной матрицей. Такие системы получаются при моделировании некоторых инженерных задач, а также при численном решении краевых задач для дифференциальных уравнений.

Запишем систему уравнений в виде:

На главной диагонали матрицы этой системы стоят элементы над ней - элементы под ней - элементы При этом обычно все коэффициенты b_i не равны нулю.

Метод прогонки состоит из двух этапов - прямой прогонки (аналога прямого хода метода Гаусса) и обратной прогонки (аналога обратного хода метода Гаусса). Прямая прогонка состоит в том, что каждое неизвестное х_i выражается через x_i+1 с помощью прогоночных коэффициентов AA_i, ВВ_i:

(1)

Из первого уравнения системы найдём

С другой стороны, по формуле (1) Приравнивая коэффициенты в обоих выражениях для х₁, получаем

(2)

Из второго уравнения системы выразим х₂ через х₃, заменяя x_i по формуле (1):

Отсюда найдём

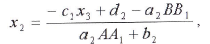
или

Аналогично можно вычислить прогоночные коэффициенты для любого
номера i:

(3)

Обратная прогонка состоит в последовательном вычислении неизвестных x_i.Сначала нужно найти х_n.Для этого воспользуемся выражением (1) при i=n-1и последним уравнением системы. Запишем их:

Отсюда

Далее, используя формулы (1) и выражения для прогоночных коэффициентов (2), (3), последовательно вычисляем все неизвестные x_i для i=n-1, n-2,...,1.

При анализе алгоритма метода прогонки надо учитывать возможность деления на нуль в формулах (3). Можно показать, что при выполнении условия преобладания диагональных элементов, т.е. если

причём хотя бы для одного значения iимеет место строгое неравенство, деления на нуль не возникает, и система имеет единственное решение.

Приведённое условие преобладания диагональных элементов обеспечивает также устойчивость метода прогонки относительно погрешностей округлений. Последнее обстоятельство позволяет использовать метод прогонки для решения больших систем уравнений. Заметим, что данное условие устойчивости прогонки является достаточным, но не необходимым. В ряде случаев для хорошо обусловленных систем метод прогонки оказывается устойчивым даже при нарушении условия преобладания диагональных элементов.

Задания: выполнить задание 5 ИДЗ№1.