Цель - ознакомить студентов с методом Ньютона решения алгебраических уравнений.
Метод касательных (Метод Ньютона)
Пусть корень уравнения f(x)=0 отделен на отрезке [a,b], причем f'(x) и f''(x) непрерывны и сохраняют свои знаки на этом отрезке. Тогда, как было сказано выше, возможны четыре случая, графически изображенные на рис.1 а)-г).
Геометрически метод Ньютона эквивалентен замене дуги кривой ММ' касательной, проведенной к некоторой точке данной кривой.

1. Рассмотрим случай f(a)f"(x)<0, которому соответствуют графики изображенные на рис.1 б) или 1 в). В этом случае, приближение к корню А происходит со стороны точки b (см. рис.2). Касательные проводятся в точках M0, M1, M2,....Пересечением касательных с осью 0х является последовательность точек b0,b1,b2, которая сходится к точному корню А. Уравнение касательной к функции f(x) в точке Mn с координатами (bn,f(bn)) имеет вид:
 (8)
(8)
Полагая y=0, x=bn+1 получаем
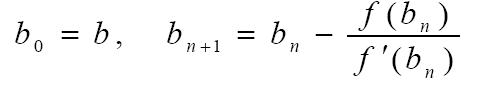 (9)
(9)
Заметим, что если бы мы в данном случае провели касательную в точке (a,f(a)), то точка пересечения этой касательной с осью 0х лежала бы вне отрезка [a,b], и требуемой сходимости к корню не наблюдалось бы.
2. В случае f(a)f"(x)>0 (см. рис.1 а или 1г) приближение к корню А происходит со стороны точки a, а последовательность точек определяется по рекуррентной формуле
 (10)
(10)
Для оценки погрешности метода касательных будем предполагать, что обе производные функции f(x) непрерывны и сохраняют свой знак на отрезке [a,b]. Тогда, если А - точный корень, а xn - приближение к корню, то оценка погрешности может быть вычислена по одной из следующих формул
 (11)
(11)
 (12)
(12)
где 
Если  , то формула (12) упрощается
, то формула (12) упрощается
 (12*)
(12*)
Пример. Вычислить приближенно по методу касательных с точностью до пяти десятичных знаков после запятой больший отрицательный корень уравнения x3 -12x-8 = 0.
Решение. Графически отделяя корни данного уравнения, заключаем, что уравнение имеет три действительных корня; больший отрицательный корень принадлежит отрезку [-1,0]. Укажем отрезок меньшей длины, на котором находится корень; это отрезок [-0,7;-0,65], поскольку f(-0,7) = 0,057, f(-0,65)= -0,474625.
Т.к. f"(x) = 6x, то очевидно для отрицательных x имеем f"(x)<0, то выполнено условие f(a)f"(x)<0, поэтому в качестве нулевого приближения берем b0=-0,65, а последующие приближения вычисляем по формуле (9).
Описанный выше процесс решения удобно оформить в виде вычислительного бланка.

Процесс прервался, после третьего шага, т.к. мы достигли нужную точность, которая в данном случае может быть рассчитана по формуле (12*). Приближенное значение корня А=-0,694593±0,000001.
Задания. Выполнить задание 2.2 ИДЗ№1.






