Геометрическая постановка задачи. Найти в области решений системы линейных неравенств точку, через которую проходит линия уровня, соответствующая наибольшему (наименьшему) значению линейной функции с двумя переменными.
Последовательность действий:
1. Построить область допустимых решений системы линейных неравенств 
Если область непустая, то можно говорить о целесообразности нахождения в ней наибольшего и наименьшего значений функции.


 В
В
| |||
 | |||
 A
A

|

|
 х
х
2. Построить градиент  и одну из линий уровня
и одну из линий уровня  функции
функции  .
.
3. Параллельным перемещением прямой  в направлении вектора
в направлении вектора  геометрически найти две точки:
геометрически найти две точки:
· точку А «входа» в область. Эта точка определяет точку наименьшего значения функции 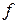 ;
;
· точку В «выхода» из области. Эта точка определяет точку наибольшего значения функции 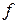 .
.
4. Найти координаты точки А, решая систему уравнений прямых, пересекающихся в точке А, и вычислить наименьшее значение функции  . Аналогично – для точки В и наибольшего значения функции
. Аналогично – для точки В и наибольшего значения функции  .
.
Пример. Найти наибольшее и наименьшее значения функции  в области решений системы линейных неравенств
в области решений системы линейных неравенств

Решение. Построим область решений системы линейных неравенств. Для этого построим полуплоскости и найдём их пересечение. В качестве контрольной точки возьмём точку  , которая не принадлежит граничным прямым.
, которая не принадлежит граничным прямым.

 у
у 





 1
1 


 О 2 x
О 2 x

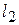

Прямая ( )
)  , точки для построения
, точки для построения  и
и  . Так как
. Так как  верно, то полуплоскость обращена в сторону точки
верно, то полуплоскость обращена в сторону точки  .
.
Прямую (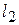 )
)  строим по точкам
строим по точкам 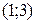 и
и  ; неравенство
; неравенство  верное, полуплоскость направлена к началу координат.
верное, полуплоскость направлена к началу координат.
Прямая ( )
)  построена по точкам
построена по точкам  и
и  ; полуплоскость обращена в сторону
; полуплоскость обращена в сторону  .
.
Неравенства  и
и  показывают, что искомая область (пересечение всех полуплоскостей) находится в первой координатной четверти.
показывают, что искомая область (пересечение всех полуплоскостей) находится в первой координатной четверти.
2. Построим градиент функции  – вектор с координатами
– вектор с координатами  с началом в точке
с началом в точке  . Перпендикулярно градиенту построим одну из линий уровня.
. Перпендикулярно градиенту построим одну из линий уровня.
3. Параллельным движением линии уровня в направлении градиента  найдем точку ее «входа» в область – это точка О(0,0). Вычислим значение функции в этой точке:
найдем точку ее «входа» в область – это точка О(0,0). Вычислим значение функции в этой точке: 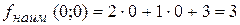 .
.
4. Продолжая движение линии уровня в направлении градиента  , найдем точку «выхода» линии уровня из области – это точка А. Для определения её координат решим систему уравнений прямых
, найдем точку «выхода» линии уровня из области – это точка А. Для определения её координат решим систему уравнений прямых 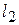 и
и  :
:  Решение системы уравнений
Решение системы уравнений  и
и  .
.
5. Вычислим значение функции в точке 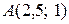 :
:  .
.
Ответ:  ,
,  .
.
Контрольные вопросы по теме 3:
1. В чём заключается геометрический смысл функции двух переменных?
2. Приведите схему графического решения линейного неравенства с двумя переменными.
3. Как построить многоугольник решений?
4. Опишите основные этапы графического решения задачи нахождения наибольшего и наименьшего значений линейной функции в области.









