Постановка задачи. Пусть на плоскости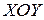 
замкнутая ограниченная область 
задаётся системой неравенств вида
.
Требуется найти в области точки, в которых функция 
принимает наибольшее и наименьшее значения.
Важной является задача нахождения экстремума, математическая модель которой содержит линейные ограничения (уравнения, неравенства) и линейную функцию 
.
Постановка задачи. Найти наибольшее и наименьшее значения функции
(1)
при ограничениях
(2)
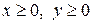. (3)
Поскольку для линейной функции многих переменных нет критических точек внутри области , то оптимальное решение, доставляющее целевой функции экстремум, достигается только на границе области. Для области, заданной линейными ограничениями, точками возможного экстремума являются угловые точки. Это позволяет рассматривать решение задачи графическим методом.
