График функции двух переменных. Линии уровня. Частные производные первого порядка и градиент функции двух действительных переменных. Свойства градиента. Графическое решение системы линейных неравенств. Графическое нахождение наибольшего и наименьшего значений линейной функции в области.
Основные термины: график, прямая, плоскость, линии уровня, частные производные, градиент, многоугольник решений.
1) Функцией двух переменных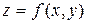 
называется правило 
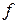, по которому каждой упорядоченной паре чисел 
из некоторого множества 
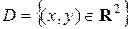поставлено в соответствие единственное число 
из множества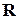 
.
Для функции двух переменных 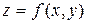областью определенияявляется некоторое множество точек на плоскости 
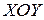, а областью значений – промежуток на оси 
.
Графиком функции двух переменных 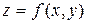является поверхность в трехмерном пространстве, состоящая из точек 
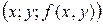, где пары 
принадлежат области определения функции .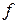
Для наглядного представления функции двух переменных применяются линии уровня. Линией уровня функции 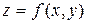называется множество таких точек в области определения (на плоскости 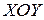), для которых значение функции постоянно и равно 
. т.е. 
.
Пример. Для функции 
построить график и линии уровня. Записать уравнение линии уровня, проходящей через точку 
.
Графиком линейной функции 
является плоскость в пространстве. Для функции график представляет собой плоскость, проходящую через точки 
, 
, 
.
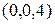Линиями уровня функции являются параллельные прямые, уравнение которых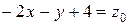 
. Для линейной функции двух переменных 
линии уровня задаются уравнением 
и представляют собой семейство параллельных прямых на плоскости.
Y
4 4
0 1 2 Х
График функции
Линии уровня функции
2) Градиент функции двух переменных
Градиентом функции 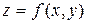в точке 
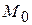называется вектор с началом в точке 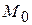, координаты которого равны значениям частных производных в точке : 
.
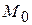