Для графического решения данной задачи необходимо уметь решать графически системы линейных неравенств с двумя переменными.
Решением линейного неравенства с двумя переменными 
называется множество пар значений переменных 
, которые удовлетворяют неравенству. Геометрически решением линейного неравенства является полуплоскость, границей которой является прямая 
.
Порядок действий:
1) записать уравнение и построить на плоскости граничную прямую;
2) выбрать искомую полуплоскость, координаты точек в которой удовлетворяют заданному неравенству. Для этого подставляют в неравенство координаты точки с известными координатами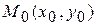 
, не лежащей на граничной прямой. Если получится верное числовое неравенство, то искомая полуплоскость та, которая содержит точку 
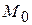(в противном случае берется другая полуплоскость). Плоскость выделяется штриховкой.
0 
Отметим, что неравенство 
определяет правую координатную полуплоскость (от оси 
), а неравенство 
– верхнюю координатную полуплоскость (от оси 
).
Пример. Решить графически неравенство 
.
Запишем уравнение граничной прямой 
и построим её по двум точкам, например, 
и 
. Прямая делит плоскость на две полуплоскости.
 |
0 2
–4
Координаты точки 
удовлетворяют неравенству (
– верно), значит, и координаты всех точек полуплоскости, содержащей точку , удовлетворяют неравенству. Решением неравенства будут координаты точек полуплоскости, расположенной справа от граничной прямой , включая точки на границе. Искомая полуплоскость на рисунке выделена.
Решением системы 
линейных неравенств 
называется множество пар значений переменных , которые удовлетворяют одновременно всем неравенствам. Геометрически решением системы линейных неравенств является область на плоскости, координаты точек которых лежат в пересечении полуплоскостей.
Решение 
системы неравенств называется допустимым, если его координаты неотрицательны , . Множество допустимых решений системы неравенств образует область, которая расположенав первой четверти координатной плоскости.
Пример. Построить область решений системы неравенств 
Решениями неравенств является:
1) 
– полуплоскость, расположенная левее и ниже относительно прямой (
) 
;
2) 
– полуплоскость, расположенная в правой-нижней полуплоскости относительно прямой (
) 
;
3) 
– полуплоскость, расположенная правее прямой (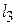
) 
;
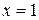4) – полуплоскость выше оси абсцисс, то есть прямой (
) 
.
3
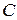
1 В
0 
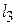
Область допустимых решений данной системы линейных неравенств – это множество точек, расположенных внутри и на границе четырехугольника 
, являющегося пересечением четырех полуплоскостей.
Геометрическое изображение линейной функции (линии уровня и градиент)
Зафиксируем значение 
, получим уравнение 
, которое геометрически задаёт прямую. В каждой точке прямой функция принимает значение 
и является линией уровня. Придавая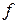 
различные значения, например, 
,..., получим множество линий уровня – совокупность параллельных прямых.
Построим градиент – вектор 
, координаты которого равны значениям коэффициентов при переменных в функции 
. Данный вектор: 1) перпендикулярен каждой прямой (линии уровня) 
; 2) показывает направление возрастания целевой функции.
Пример. Построить линии уровня и градиент функции 
.
 |
 |
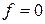
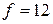
Линии уровня при 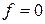, , 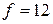– это прямые 
, 
, 
, параллельные друг другу. Градиент – это вектор , перпендикулярный каждой линии уровня.
