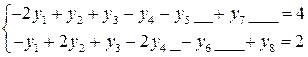

Решение двойственной задачи приводим в виде симплекс-таблиц.
Расчётная таблица М (симплекс) метода. Двойственная задача. Нулевая итерация
| 
| 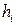
| 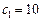
|  
| 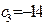
| 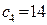
| 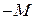
| 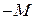
|  
| ||
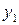
| 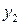
| 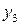
| 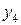
| 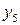
| 
| 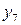
| 
| ||||
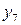
| 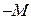
| -2 | -1 | -1 | |||||||

| 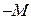
| -1 | -2 | -1 | |||||||
| Индексная строка | -6М | 3М-10 | -3М+20 | -2М+14 | 3М-14 | М | М |
Расчётная таблица М (симплекс) метода. Двойственная задача. Первая итерация
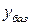
| 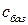
| 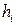
| 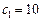
|  
| 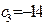
| 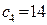
| 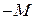
|  
| ||
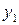
| 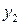
| 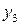
| 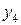
| 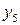
| 
| 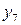
| ||||
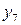
| 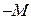
| -3/2 | 1/2 | -1 | 1/2 | |||||
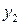
| -20 | -1/2 | 1/2 | -1 | -1/2 | |||||
| Индексная строка | -3М-20 | 3М/2 | -6-М/2 | М | 10-М/2 |
Расчётная таблица симплекс метода. Двойственная задача. Вторая итераци я
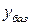
| 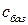
| 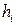 (план) (план)
| 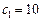
|  
| 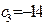
| 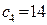
| |||
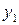
| 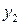
| 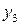
| 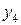
| 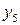
| 
| ||||
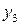
| -14 | -3 | -2 | Двойственный симплекс метод | |||||
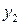
| -20 | -2 | -1 | -1 | |||||
| Индексная строка | -44 | ||||||||
| -6 | -6 |  
|
Если все критерии  индексной строки положительные, а план (
индексной строки положительные, а план (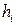 ) отрицателен, то для нахождения оптимального решения воспользуемся двойственным симплекс-методом. При двойственном симплекс методе из базиса выводим переменную с максимальным по модулю отрицательным значением
) отрицателен, то для нахождения оптимального решения воспользуемся двойственным симплекс-методом. При двойственном симплекс методе из базиса выводим переменную с максимальным по модулю отрицательным значением 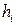 и вводим в базис переменную с минимальным отношением
и вводим в базис переменную с минимальным отношением  , причём
, причём 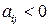 . Введём в базис переменную
. Введём в базис переменную 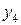 .
.
Расчётная таблица симплекс метода. Двойственная задача. Третья итерация.
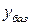
| 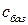
| 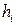 (план) (план)
| 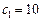
| 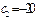
| 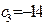
| 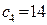
| ||
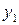
| 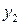
| 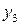
| 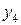
| 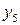
| ||||
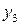
| -14 | -3 | -2 | |||||
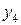
| -1 | -1 | -1 | |||||
| Индексная строка | -56 |
В индексной строке симплекс таблицы все критерии  положительны. Планы
положительны. Планы 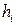 также положительны. Следовательно, получен оптимальный план двойственной задачи. Переменные
также положительны. Следовательно, получен оптимальный план двойственной задачи. Переменные 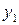 и
и 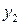 не входят в базис. Все свободные переменные считаются нулевыми. Поэтому
не входят в базис. Все свободные переменные считаются нулевыми. Поэтому 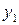 и
и 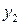 равны нулю.
равны нулю. 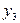 =6, и
=6, и 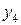 =2. Балансовые переменные
=2. Балансовые переменные 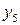 и
и  .также являются свободными и равны нулю. Таким образом, оптимальный план двойственной задачи следующий:
.также являются свободными и равны нулю. Таким образом, оптимальный план двойственной задачи следующий: 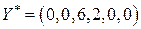 . Минимальное значение целевой функции
. Минимальное значение целевой функции 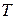 =-
=-  =56.☻
=56.☻
Сравнение результатов решения исходной и двойственной задач
1. Если исходная задача имеет оптимальное решение, то и двойственная ей задача имеет оптимальное решение. Причём, максимум целевой функции 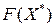 совпадает с минимумом целевой функции
совпадает с минимумом целевой функции 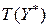 .
.
2. В индексной строке оптимального решения двойственной задачи содержится оптимальное решение исходной задачи и наоборот. Например: 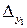 =18=
=18= 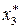 ;
;  =6=
=6=  ;
; 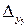 =14=
=14= 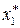 ;
; 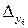 =0=
=0= 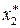 .
.