Математическое программирование связано с управлением производственными процессами, например, нахождением наиболее рационального использования сырья и материалов, определением наиболее выгодных производственных режимов, повышением эффективности работы транспорта и т.д.
Математическим программированием называется раздел математики, в котором изучаются методы нахождения максимума или минимума целевой функции 
конечного числа переменных 
, при условии, что переменные удовлетворяют конечному числу дополнительных условий (ограничений), имеющих вид уравнений и/или неравенств. Накладывается также условие неотрицательности переменных .
Если целевая функция и ограничения линейны, то имеем задачу линейного программирования (ЗЛП). Если или целевая функция и/или ограничения являются нелинейными, то это задача нелинейного программирования (ЗНП).
Математической моделью экономической задачи называется совокупность математических соотношений, описывающих рассматриваемый экономический процесс. Это адекватный ”перевод” всех существенных сведений о решаемой проблеме на язык математики в виде уравнений тождеств и неравенств. Модель включает: целевую функцию, ограничения задачи и условие неотрицательности переменных. Для составления математической модели необходимо: 1) выбрать переменные задачи; 2)составить систему ограничений; 3) задать целевую функцию.
Переменными задачи называются величины , которые полностью характеризуют экономический процесс. Их обычно записывают в виде вектора 
,где 
.
Системой ограничений задачи называется совокупность уравнений и/или неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов или других экономических условий, например условия положительности переменных. В общем случае они имеют вид:
.
В случае ЗЛП ограничения имеют вид 
Целевой функцией 
называют функцию от переменных задачи, которая характеризует качество осуществления задачи и экстремум которой (максимум или минимум) требуется найти. Для задачи линейного программирования целевая функция имеет вид: 
Допустимым решением (планом) ЗЛП называется любой n-мерный вектор , удовлетворяющий системе ограничений и условиям неотрицательности . Множество допустимых решений образуют область допустимых планов или решений. Область 
допустимых планов, если она не является пустым множеством, ограничена выпуклым многогранником (при n=2- выпуклым многоугольником), вершины которого называются опорными планами.
Оптимальным решением (планом) называется такое допустимое решение, при котором целевая функция достигает экстремума. Из свойств линейной функции следует, что её максимум или минимум не может достигаться во внутренних точках области. Поэтому оптимальный план совпадает с одним из опорных планов.
Если ищется максимум целевой функции, а все ограничения задачи записаны с помощью знака 
или при нахождении минимума целевой функции все ограничения записаны с помощью знака 
, то задача записана в стандартной форме ЗЛП. Если все ограничения задачи записаны в форме уравнений с помощью знака =, то имеем каноническую форму ЗЛП.
Переход от стандартной к канонической форме осуществляется путём прибавления к каждому ограничению задачи новых неотрицательных балансовых переменных 
(в случае знака ) и вычитания- (в случае знака ). Число вводимых дополнительных переменных равно числу преобразуемых неравенств.
Переход от канонической к стандартной форме осуществляется исключением из ограничений задачи и целевой функции неотрицательных переменных, причём ограничения должны быть предварительно разрешены относительно исключаемых переменных.
Отыскание минимума целевой функции «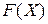
»можно заменить отысканием максимума функции «
».
