Методом искусственного базиса (симплекс-методом) решить ЗЛП:
.
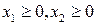Переходим к канонической форме задачи, вводя в каждое ограничение- неравенство дополнительные балансовые переменные (чтобы можно было заменить знаки неравенства знаками =).
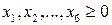
Так как в первом и четвертом ограничении нет базисных переменных, то в эти уравнения вводим фиктивные (искусственные) переменные 
. Эти же переменные войдут и в целевую функцию 
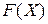с коэффициентами - 
. Получим расширенную - задачу:
Заполняем расчётную таблицу (симплекс) метода и подсчитываем значение индексных строк (пункт 3)
.Расчётная таблица (симплекс) метода. Нулевая итерация.
| № итерации | № строки | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| 
| |
| 
| 
| 
| 
| 
| 
| 
| |||||||
|
| 
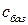
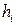
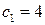
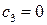
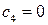
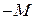
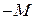
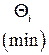
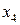
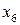
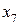
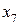
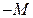
| -1 | ||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
|
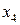
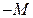
| -1 | ||||||||||||
| Индексные строки | -24 M | -3M | -3M | M | M | |||||||||
| -4 | -2 | |||||||||||||
Так как наиболее отрицательное значение показателя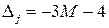 
расположено в столбце , то переменную вводим в базис и исключаем из базиса ту переменную, для которой критерий 
будет минимальным. Критерий минимальный для четвёртой строки расчётной таблицы, базисная переменная которой . Эту переменную выводим из базиса. Таким образом, у нас разрешающим столбцом является первый столбец (по индексу ), а разрешающей строкой- четвёртая строка. (p=1; q=4).
Т.к. коэффициент при разрешающем элементе 
, разрешающая строка остаётся без изменения. Чтобы получить нули в первой, второй и третьей строке первого столбца, от первой строки отнимем удвоенное значение четвёртой строки, а от второй и третей строки отнимем четвёртую. При исключении из состава базисных вектора условной переменной , из расчётной таблицы исключаем и столбец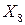 
.Пересчёт коэффициентов 
можно проводить и по правилу прямоугольника. Заполняем расчётную таблицу первой итерации
Расчётная таблица (симплекс) метода. Первая итерация
| № ите ра ции | № ст ро ки |
|
|
|
| 
| 
| 
| 
| 
|
|
|
|
|
|
|
|
|
| |||||
|
|
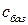
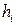
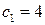
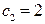
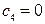
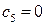
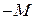
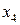
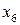
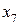
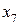
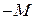
| -18 | -3 | -1 | |||||||
|
| |||||||||||
|
| -1 | ||||||||||
|
| --1 | ||||||||||
| Индексные строки | 18М | 3М | М | -2М | |||||||
| +56 | +6 | -4 |
В состав базисных вводим вектор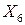 
и из базиса выводим вектор 
фиктивной переменной. Столбец также исключаем из расчётной таблицы. Новое значение разрешающей (первой) строки получим путём деления на два всех её членов. Новые значения второй и четвёртой строк получим путём вычитания из старых значений преобразованной разрешающей строки. К третьей строке прибавляем новую разрешающую строку. (Пересчёт коэффициентов можно производить и по правилу прямоугольника.) Получим:
Расчётная таблица симплекс-метода. Вторая итерация.
| № ите ра ции | № ст ро ки |
|
|
|
|
|
|
|
|
| 
|
|
|
|
|
|
|
| ||||||
|
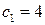
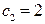
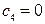
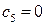
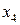
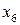
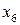
| -9 | -3/2 | -1/2 | ||||||||
|
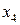
| 3/2 | ½ | |||||||||
|
| ½ | ½ | |||||||||
|
| ½ | -1/2 | ----- | ||||||||
| Индексная строка | -2 |
Расчётная таблица симплекс-метода. Третья итерация.
| № ите а ции | № ст ро ки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
|
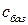
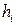
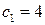
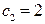
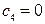
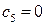
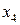
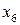
| -2 | ---- | |||||||||
|
| |||||||||||
|
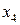
| -1 | ||||||||||
|
| -1 | ----- | |||||||||
| Индексная строка | -4 |
Т.к. в индексной строке третьей итерации имеется отрицательный критерий 
, то полученный план не является оптимальным и его можно улучшать. В базис вводим вектор 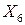и выводим из базиса вектор 
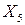. Разрешающая третья строка остаётся без изменений, т.к. разрешающий элемент равен 1. Первая строка преобразуется путем прибавления к её членам элементов третьей строки, умноженным на 2, от второй строки отнимаем третью строку, а к элементам четвёртой строки прибавляем элементы третьей строки. Получаем новый план (четвёртая итерация)
Расчётная таблица симплекс-метода. Четвёртая итерация.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
| |||||||||
|
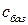
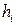
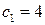
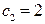
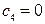
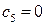
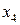
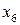
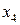
| -1 | ||||||||
|
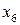
| -1 | ||||||||
|
| |||||||||
| Индексная строка |
Индексная строка последней симплекс- таблицы не содержит отрицательных критериев. Получен оптимальный план.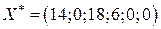 
. Максимальное значение целевой функции 
Экономическое истолкование решения задачи может быть таким: производится 14 единиц продукции первого вида и не производится продукция второго вида. Неиспользованные остатки сырья первого, второго, третьего и четвёртого видов составляют соответственно 18; 6; 0 и 0 единиц. Максимальная прибыль от реализации продукции составляет 56 (денежных) единиц.☻
