Основным аналитическим методом решения задач линейного программирования является симплекс- метод. Он применяется при решении ЗЛП, представленных в канонической форме. Предварительно система уравнений (ограничений задачи) должна быть разрешена относительно базисных переменных.
Базисная переменная входит только в одно уравнение- ограничение задачи с коэффициентом равным единице, и не входит в другие уравнения – ограничения. Базисных переменных должно быть столько же, сколько ограничений в задаче. Остальные переменные называются свободными. Базисные переменные можно выделить, выполняя симплекс- преобразования, но часто эти преобразования весьма громоздки. Чтобы их избежать, применяют метод искусственного базиса.
Метод искусственного базиса состоит в замене исходной задачи с недостающим числом базисных переменных расширенной задачей с дополнительными (искусственными или фиктивными переменными), затем исключаемыми из базиса. Чтобы фиктивные переменные исключались из базиса, добавим их и в целевую функцию с очень большим отрицательным коэффициентом -М (штрафом). В процессе улучшения плана фиктивные переменные выводятся из базиса в первую очередь и исключаются из симплекс-таблицы.
Симплексные преобразования позволяют переходить от одного опорного плана к другому, по крайней мере, не худшему исходного. Число таких преобразований конечно.
При симплекс-методе производится преобразование базиса путём исключения из его состава одного из базисных векторов и ввода в состав базиса некоторого свободного вектора.Какой вектор ввести в состав базисных, и какой исключить из состава, определяем при помощи 
и 
критериев. Алгоритмпоиска оптимального решения заключается в том, чтобы последовательными заменами базиса добиться неотрицательности свободных членов в ограничениях и неположительности .критериев оптимальности. При выполнении этих условий максимальное значение целевой функции находится в столбце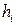 
свободных членов индексной строки. Все свободные члены при этом равны 0.
Симплексные преобразования производим по шагам (которые называют итерациями) в симплекс таблицах.
Описание симплекс- таблицы. Симплекс- таблица имеет на три (четыре для М- задачи) строки больше числа ограничений ЗЛП и на шесть столбцов больше, чем в расширенной задаче (М- задаче).
Во второй строке симплекс-таблицы помещаем переменные задачи 
. В первой строке записываем коэффициенты при соответствующих переменных в целевой функции.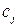 
Последняя индексная строка (или строки) служит для оценки оптимальности составленного плана. На первой позиции этой строки помещаем значение целевой функции 
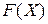, а на остальных-критерии .
В первом столбце записываем номер итерации. Во втором столбце записываем номер текущей строки. В третьем столбце записываем базисные переменные, 
отвечающие данному 
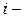му ограничению. Коэффициенты при соответствующих базисных переменных 
.помещаем в четвёртой столбце. В пятом столбце записываем свободные члены уравнений-ограничений (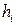 (план)). Остальные столбцы состоят из коэффициентов 
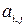ограничений М-задачи. В последнем столбце помещаем значения критериев .
