1. Случайная величина X задана функцией распределения

Найти вероятность того, что в результате испытания величина X примет значение, заключенное в интервале 
2. Случайная величина X задана функцией распределения

Найти вероятность того, что в результате четырех независимых испытаний величина X ровно три раза примет значение, принадлежащее интервалу 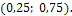
3. Дана функция распределения НСВ X

Найти плотность распределения  .
.
4. Случайная величина X задана интегральной функцией распределения

Требуется: а) найти дифференциальную функцию распределения (плотность вероятности); б) найти математическое ожидание и дисперсию X; в) построить графики интегральной и дифференциальной функций распределения.
Вопросы для самоконтроля
1. Дайте понятие непрерывной случайной величины. Приведите примеры.
2. Как задать закон распределения непрерывной случайной величины?
3. В чем заключается вероятностный смысл интегральной функции распределения?
4. В чем заключается вероятностный смысл дифференциальной функции распределения?
5. Как связаны между собой дифференциальная и интегральная функции распределения?
6. Назовите свойства интегральной функции распределения. Каковы особенности ее графика?
7. Назовите свойства дифференциальной функции распределения. Каковы особенности ее графика?
8. Как найти вероятность попадания непрерывной случайной величины заданный промежуток с помощью интегральной и с помощью дифференциальной функции распределения?






