Задача 1. Случайная величина X задана плотностью распределения 
в интервале (0;l); вне этого интервала 
. Найти математическое ожидание величины X.
.
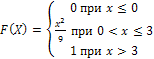Решение: Используем формулу 
. Подставив 
и 
, получим 
.
Ответ: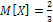 
.
Задача 2. Случайная величина X задана интегральной функцией распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X.
Решение. Найдем дифференциальную функцию распределения.
Воспользовавшись формулами для вычисления числовых характеристик непрерывной случайной величины, получим:
.
.
.
.
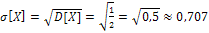Ответ: 
.
Задача 3. Случайная величина X задана плотностью распределения 
в интервале (0;2); вне этого интервала . Найти начальные и центральные моменты первого, второго, третьего и четвертого порядков.
Решение: По формуле 
найдем начальные моменты:
; 
; 
; 
.
Найдем центральные моменты. Центральный момент первого порядка любой случайной величины равен нуль.
Воспользуемся формулами, выражающими центральные моменты через начальные моменты:
;
;
.
Ответ: 
; 
; 
; 
; 
; 
; 
; 
.
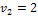