Выборочный метод - один из основных методов математической статистики. Его сущность заключается в том, что изучение большой совокупности объектов относительно некоторого количественного признака X происходит по сравнительно небольшому числу случайно отобранных объектов.
Генеральной совокупностью называется множество всех изучаемых объектов, из которых производится выборка.
Выборочной совокупностью (выборкой) называется множество объектов, отобранных для изучения из генеральной совокупности.
Выборка должна быть организованна случайным образом, чтобы правильно представлять генеральную совокупность.
Объемом совокупности называется количество объектов в совокупности. Объем выборки п, как правило, значительно меньше объема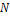 
генеральной совокупности: 
.
Данные выборки записываются в виде таблицы, называемой статистическим распределением выборки:
| 
| 
| 
| … | 
|
| 
| 
| 
| … | 
|
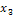
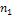
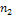
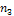
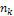
В первой строке перечислены все наблюдаемые значения признаках в порядке их возрастания (или убывания). Они называются вариантами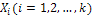 
. Во второй строке указаны частоты 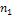, соответствующих вариант они показывают, сколько раз наблюдалось каждое значение признака .
Очевидно, что сумма всех частот , равна объему выборки 
:
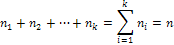
Основные числовые характеристики выборки:
1. Средняя выборочная (среднее взвешенное значение признака в выборке).
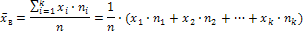
2. Дисперсия выборочная. Характеризует разброс (рассеяние) значений вариант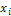 
, от выборочного среднего значения 
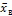, измеряется в квадратных единицах признака .
.
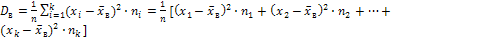3. Среднее квадратическое отклонение выборки - характеристика рассеяния значений признака в выборке от среднего выбранного в единицах признака .
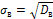
Для вычисления дисперсии используется также другая, часто более удобная формула 
, где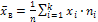 
; 
.
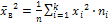Интервальной называют оценку, которая определяется двумя числами - концами интервала, покрывающего оцениваемый параметр.
Доверительным называют интервал, который с заданной надежностью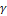 
покрывает заданный параметр.
Пример
Задача. Даны выборочные варианты 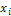и соответствующие им частоты количественного признака :
1. Найти выборочную среднюю, дисперсию и среднее квадратическое отклонение.
2. Считая, что количественный признак X распределен по нормальному закону и что выборочная дисперсия равна генеральной дисперсии, найти доверительный интервал для оценки математического ожидания с надежностью 
.
Решение. 1. Объем выборки: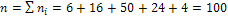 
.
Средняя выборочная:
.
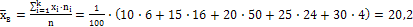Выборочная дисперсия:
.
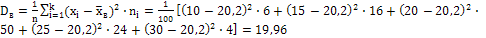Второй способ вычисления дисперсии:
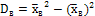, где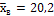 
.
Средняя выборочная квадратов значений признака:
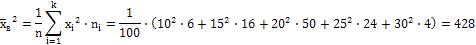
Тогда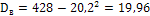 
, что совпадает с результатом первого способа.
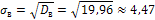
2. Доверительный интервал для оценки генеральной средней.
Найденные характеристики выборки 
, 
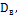
лишь приближенно характеризуют генеральную совокупность и могут оказаться далекими от соответствующих характеристик генеральной совокупности: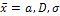 
. Поэтому для последних используют интервальные оценки, когда неизвестная характеристика заключена в некотором интервале с заданной надежностью (вероятностью) 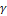. Такой интервал называется доверительным. Значения надежности берутся, как правило, высокими: 0,9; 0,95; 0,99 или 0,999, что соответственно составляет 90; 95; 99; 99,9%.
Пусть количественный признак X в генеральной совокупности распределен по нормальному закону, причем среднее квадратическое отклонение «
» этого распределения известно. Тогда с вероятностью 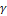доверительный интеграл, заданный формулой
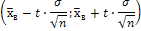
показывает неизвестное математическое ожидание. Здесь число t находится из соотношения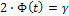 
с помощью таблицы интегральной функции Лапласа.
В данной задаче , поэтому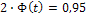 
, а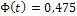 
. По таблице приложения 3 находим 
.
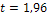По условию задачи дисперсия генеральной совокупност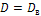и 
и 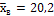. Поэтому можно найти доверительный интервал:
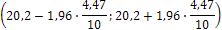
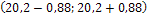
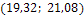
С вероятностью 0,95=95% неизвестная генеральная средняя (математическое ожидание «а») находится в этом интервале.
Ответ: ;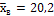 
; 
; 
.
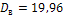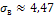