Случайной величиной называют такую величину, которая в результате испытаний примет одно и только одно из возможных значений, заранее неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены. Например, дальность полёта артиллерийского снаряда; наружный диаметр трубы.
Различают непрерывные и дискретные случайные величины.
Дискретной случайной величиной называется такая величина, которая в результате испытания принимает отдельные изолированные значения. Например: Производится 3 выстрела по цели. Случайная величина х - это число попаданий в цель, тогда х может принимать значения: 0,1, 2, 3.
Непрерывной случайной величиной называют случайную величину, которая может принимать все значения из некоторого промежутка. Значения могут быть конечными и бесконечными. Например: Время безаварийной работы станка; расход горючего на единицу расстояния; количество осадков, выпавших в сутки.
Случайные величины будем обозначать заглавными буквами конца латинского алфавита - X, Y, Z, а их возможные значения - соответствующими малыми буквами - х, у, z. Например, X - число шахматных партий, окончившихся ничейным результатом, из трёх сыгранных. В этом случае величина X может принять следующие значения: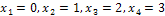 
.
Введем теперь операции над случайными величинами. Пусть имеются две случайные величины X и Y, возможными значениями которых являются соответственно 
и 
.
Суммой X+Y случайных величин X и Y называется случайная величина Z, возможные значения которой есть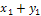 
, 
, 
, …, 
, …, 
, 
, 
, …, 
, …, 
, 
, 
, …, 
, …, 
.
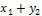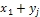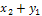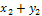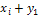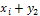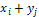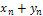Это определение следует понимать так: в результате опыта, в котором случайная величина X может принять то или иное значение, было получено число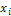 
(конкретное значение величины X), а в результате опыта, в котором уже случайная величина Y может принять то или иное значение, было получено 
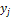(конкретное значение величины Y), после чего полученные числа складываются. Число 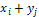и является одним из возможных значений случайной величины Z=X+Y.
Произведением XY случайных величин X и Y называется случайная величина Z, возможные значения которой есть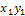 
, 
, 
, …, 
, 
, 
, …, 
, …, 
.
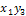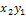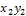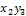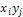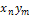Произведением CX случайной величины X на постоянную С называется такая случайная величина Z, возможные значения которой есть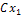 
, 
, 
, …, 
, …, 
.
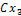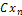Аналогично определяются разность X-Y и частное 
двух случайных величин.
Задача 1: Пусть случайная величина X может принять следующие три значения: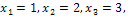 
а случайная величина Y - значения 
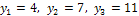. Тогда возможные значения случайной величины Z=X+Y таковы: 
, 
, 
, 
, 
, 
, 
, 
, 
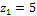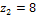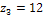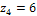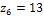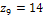, а возможные значения случайной величины Z=XY - следующие: 
, 
, 
, 
, 
, 
, 
, 
, 
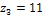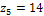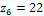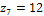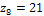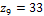. Для величины Z=5X возможными значениями являются , 
, 
.
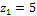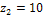