Задача 1. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте.
Решение: Дискретная случайная величина X (число отказавших элементов в одном опыте) имеет следующие возможные значения: 
(ни один из элементов устройства не отказал), 
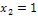(отказал один элемент), 
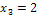(отказали два элемента) и 
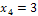(отказали три элемента).
Отказы элементов независимы один от другого, вероятности отказа каждого элемента равны между собой, поэтому применима формула Бернулли. Учитывая, что, по условию,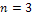 
, 
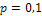(следовательно, 
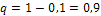), получим:
;
;
;
.
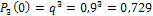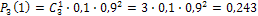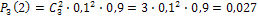Контроль: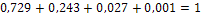 
.
Напишем искомый биноминальный закон распределения X:
Задача 2. В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны две детали. Составить закон распределения числа стандартных деталей среди отобранных.
Решение: Случайная величина X - число стандартных деталей среди отобранных деталей - имеет следующие возможные значения: , 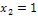и 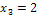. Найдем вероятности возможных значений X по формуле 
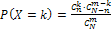, где N - число деталей в партии, 
- число стандартных деталей в партии, 
- число отобранных деталей, 
– число стандартных деталей среди отобранных.
Находим:
;
;
.
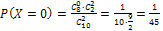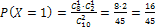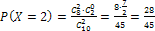Составим искомый закон распределения:
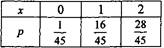
Контроль: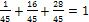 
.
Задача 3. Учебник издан тиражом 100000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Найти вероятность того, что тираж содержит ровно пять бракованных книг.
Решение: По условию, = 100000, 
= 0,0001, = 5. События, состоящие в том, что книги сброшюрованы неправильно, независимы, число велико, а вероятность мала, поэтому воспользуемся законом Пуассона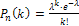 
. Найдем 
: 
.
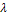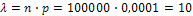Искомая вероятность равна: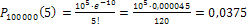 
.
Задача 4. Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути равна 0,002. найти вероятность того, что в пути будет повреждено изделий: а) ровно три; б) менее трех; в) более трех; г) хотя бы одно.
Решение: Число = 500 велико, вероятность = 0,002 мала и рассматриваемые события (повреждение изделий) независимы, поэтому имеет место формула Пуассона .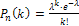
а) Найдем :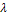 
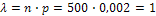. Найдем вероятность того, что будет повреждено ровно 3 (
) изделия:
.
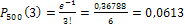б) Найдем вероятность того, что будет повреждено менее трех изделий:
.
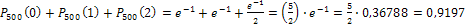в) Найдём вероятность Р того, что будет повреждено более трех изделий. События «повреждено более трех изделий» и «повреждено на более трех изделий» (обозначим это событие через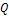 
) - противоположны, поэтому 
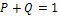. Отсюда получим: 
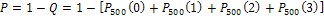. Используя результаты, полученные выше, имеем 
.
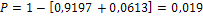г) Найдем вероятность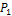 
того, что будет повреждено хотя бы одно изделие. События «повреждено хотя бы одно изделие» и «ни одно из изделий не повреждено» (обозначим это событие через 
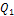) - противоположны, следовательно 
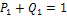. Отсюда искомая вероятность того, что будет повреждено хотя бы одно изделие, равна 
.
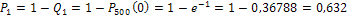