Введенные нами основные понятия векторного анализа: градиент, дивергенция, ротор – удобно представлять с помощью символического вектора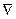 
(«набла-вектор»):
1) Произведение набла-вектора 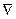на скалярную функцию u(P) дает градиент этой функции:
2) Скалярное произведение набла-вектора 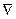на векторную функцию 
дает дивергенцию этой функции:
3) Векторное произведение набла-вектора 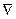на векторную функцию дает ротор этой функции:
Набла-вектор называют оператором Гамильтона.
Действия взятия градиента, дивергенции и ротора будут векторными дифференциальными операциями первого порядка. В них участвуют только первые производные от скалярных функций.
Перейдем теперь к векторным дифференциальным операциям второго порядка.
Пусть имеется скалярное поле u(P) и мы нашли градиент этого поля grad u. Поле градиента является векторным полем, и мы можем искать его дивергенцию и ротор: div grad u и rot grad u.
Если имеется векторное поле 
, то оно порождает два поля: скалярное поле 
и векторное поле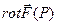 
. Следовательно мы можем находить градиент первого поля: 
и дивергенцию и ротор второго поля: 
и 
. Всего мы имеем пять векторных дифференциальных операций второго порядка. Особенно важными из них являются три, рассмотрим их.
а) 
Действительно 
Правая часть называется оператором Лапласа от функции u и обозначается 
|
С помощью набла-вектора можно записать так:
б) 
с помощью набла-вектора можно записать так:
векторное произведение одинаковых векторов = 0
в) 
с помощью набла-вектора можно записать так:
Имеем смешанное произведение трех векторов, из которых два вектора одинаковы. В этом случае такое произведение равно нулю.
Остальные две векторные операции второго порядка: 
и 
- встречаются реже.
