68. Пусть  – гравитационное поле (поле сил тяготения), которое представляет собой силу притяжения единичной массы, помещенной в точку М, массой m, находящийся в начале координат. Сила определена во всех точках, кроме начала координат и образует векторное поле – поле тяготения точечной массы m. Показать, что поле
– гравитационное поле (поле сил тяготения), которое представляет собой силу притяжения единичной массы, помещенной в точку М, массой m, находящийся в начале координат. Сила определена во всех точках, кроме начала координат и образует векторное поле – поле тяготения точечной массы m. Показать, что поле  потенциально во всем пространстве, кроме начала координат и найти его потенциал.
потенциально во всем пространстве, кроме начала координат и найти его потенциал.
69. Проверить, что поле 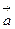 =( 3 yz+x2)
=( 3 yz+x2)  + ( 2 y2+ 3 xz)
+ ( 2 y2+ 3 xz)  +(z2+ 3 xy)
+(z2+ 3 xy)  является потенциальным, и найти его потенциал.
является потенциальным, и найти его потенциал.
70. Доказать, что векторное поле 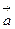 = y2
= y2  + 2 xy
+ 2 xy  +z
+z  потенциально, и найти его потенциал.
потенциально, и найти его потенциал.
71. Выяснить, является ли векторное поле 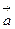 =
= 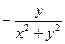
 +
+  +2
+2  потенциальным.
потенциальным.
72. Даны векторные поля: 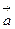 1=(y+z)
1=(y+z)  + (x+z)
+ (x+z)  +(x+y)
+(x+y)  ;
; 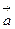 2=f(x)
2=f(x)  + f2(y)
+ f2(y)  + f3(z)
+ f3(z)  ;
; 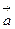 3=x
3=x  + y
+ y  +y
+y  .
.
Выяснить какие из них являются потенциальными.
73. Проверить, будет ли потенциальным поле 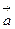 . В случае потенциальности поля найти его потенциал u(x,y,z).
. В случае потенциальности поля найти его потенциал u(x,y,z).
а) 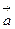 =(-2x-yz)
=(-2x-yz)  +(-2y-xz)
+(-2y-xz)  +(-2z-xy)
+(-2z-xy)  ;
;
б) 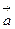 =(2x-yz)
=(2x-yz)  +(2y-xz)
+(2y-xz)  +(2z-xy)
+(2z-xy)  ;
;
в) 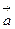 =(2x+yz)
=(2x+yz)  +(2y+xz)
+(2y+xz)  +(2z+xy)
+(2z+xy)  ;
;
г) 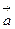 =(2x-4yz)
=(2x-4yz)  +(2y-4xz)
+(2y-4xz)  +(2z-4xy)
+(2z-4xy)  ;
;
д) 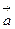 =(2x-3yz)
=(2x-3yz)  +(2y-3xz)
+(2y-3xz)  +(2z-3xy)
+(2z-3xy)  ;
;
е) 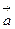 =(-3x+yz)
=(-3x+yz)  +(-3y+xz)
+(-3y+xz)  +(-3z+xy)
+(-3z+xy)  ;
;
ж) 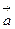 =(2x+2yz)
=(2x+2yz)  +(2y+2xz)
+(2y+2xz)  +(2z+2xy)
+(2z+2xy)  ;
;
з) 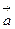 =(4x+yz)
=(4x+yz)  +(2y+xz)
+(2y+xz)  +(2z+xy)
+(2z+xy)  .
.






