Пусть функция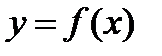 
дифференцируема на 
. 
, вообще говоря, зависит от 
, то есть 
– функция. Дифференцируя эту функцию, получаем так называемую вторую производную от 
. Производная от первой производной называется производной второго порядка или второй производной
, 
.
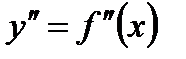Пример. Найти производную второго порядка функции 
.
Решение.
, 
.
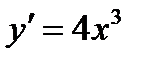Производной от второй производной называется производная третьего порядка или третья производная 
.
Вообще, производной 
-го порядка от функции 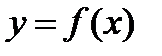называется производная первого порядка от (
)-го порядка
,
.
Обозначается в римских цифрах.
Пример 1. Найти выражение производной любого порядка функции 
, где 
.
Решение.
.
Пример 2. Найти производную -го порядка функции 
.
Решение.
,
.
Выведем формулу Лейбница, дающую возможность вычислять производную -го порядка от произведения 
.
,
,
,
,
.
надо разложить по биному Ньютона и в полученном разложении заменить показатели степени 
и 
указателями порядка производных, причем нулевые степени (
), входящие в крайние члены разложения надо заменить самими и , то есть производными нулевого порядка.
,
данное выражение носит название формула Лейбница.
