Пусть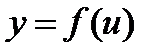 
, 
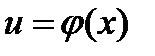, то есть 
, 
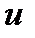– промежуточный аргумент.
Найти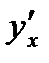 
, зная 
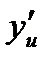и 
.
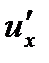Теорема. Если функция 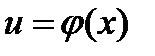имеет производную 
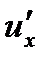в точке 
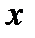, а функция 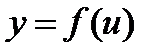имеет производную 
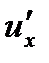в соответствующей точке 
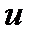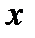, то сложная функция в данной точке имеет производную 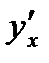, которая находится по следующей формуле
.
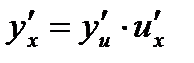Производная сложной функции равна произведению производной данной функции по промежуточному аргументу на производную промежуточного аргумента.
Доказательство. Дадим аргументу 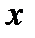приращение 
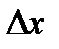, тогда 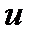и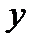 
получат соответственно 
и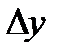 
. Предположим, что при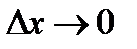 
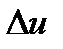не принимает значений, равных нулю.
Следовательно,
,
при 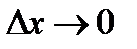получим
,
так как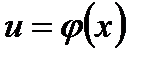 
дифференцируема, а, следовательно, и непрерывна, то при 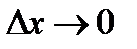также и 
, поэтому
,
, 
.
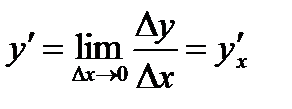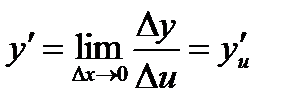
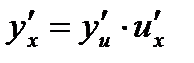Сложная функция может быть составлена из большого числа членов. Например,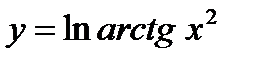 
. Здесь для того чтобы найти 
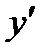по данному 
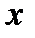, необходимо вычислить производную от: 1) 
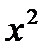; 2) 
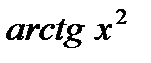; 3)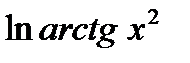 
.
В таких случаях необходимо представить, какое из действий, приводящих к значению сложной функции, является последним. При дифференцировании сложной функции та величина, над которой совершается последнее действие, принимается за промежуточный аргумент. Для 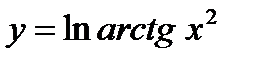последним действием является взятие натурального логарифма. Это действие совершается над функцией 
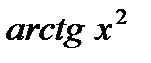. Поэтому полагаем, что промежуточным аргумент 
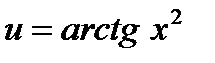, следовательно, 
, 
.
