Определение 1. Если 
имеет производную в точку 
, то есть если существует
,
при данном функция дифференцируема.
Определение 2. Функция называется дифференцируемой в интервале 
, если она дифференцируема в любой точке интервала (или отрезка).
Теорема. Если функция дифференцируема в точке 
, то она в этой точке непрерывна.
Доказательство. Пусть 
получает в точке приращение 
, соответственно 
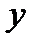получает приращение 
;
,
следовательно, функция в точке непрерывна.
Обратная теорема неверна, существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми.
Функция 
не имеет производной в точке 
.
Справа от нуля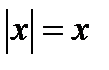 
, следовательно,
.
Слева от нуля 
, следовательно,
;
,
Следовательно, при 
отношение предела не имеет, то есть 
в точке 
не существует.
Пример. Функция 
непрерывна на (
) и при . Показать, что функция при не имеет производной.
Решение. В самом деле
,
следовательно,
,
тогда
.
Итак, в точке производной не существует (касательная к графику функции в точке совпадет с осью 
).
