Если функция 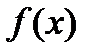 непрерывна на сегменте
непрерывна на сегменте  , дифференцируема во всех его внутренних точках и на концах сегмента обращается в нуль
, дифференцируема во всех его внутренних точках и на концах сегмента обращается в нуль  , то ее производная
, то ее производная 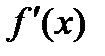 обращается в нуль хотя бы в одной внутренней точке с этого сегмента.
обращается в нуль хотя бы в одной внутренней точке с этого сегмента.
Доказательство. Так как 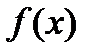 непрерывна на сегменте, следовательно, она достигает на этом сегменте своего наибольшего значения
непрерывна на сегменте, следовательно, она достигает на этом сегменте своего наибольшего значения  и наименьшего значения
и наименьшего значения  (свойства непрерывных функций).
(свойства непрерывных функций).
Если  , то
, то 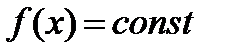 на
на  . Тогда
. Тогда 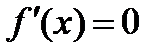 в любой точке
в любой точке  .
.
Пусть  , то одно из этих значений, например,
, то одно из этих значений, например,  . Тогда наибольшее значение
. Тогда наибольшее значение  достигается в точке
достигается в точке  :
:  . Следовательно,
. Следовательно,  , то есть
, то есть  , так как
, так как  . Тогда по теореме Ферма
. Тогда по теореме Ферма  .
.
Если  пересекает ось
пересекает ось  в точке
в точке  и
и  , то между
, то между  и
и  существует точка
существует точка  ,
,  , в которой касательная параллельна оси
, в которой касательная параллельна оси  (рис. 7).
(рис. 7).

|
| Рисунок 7 – |
Пример. На  задана функция
задана функция  . Проверить выполнение теоремы Ролля.
. Проверить выполнение теоремы Ролля.
Решение. Функция  на
на  удовлетворяет условиям теоремы Ролля, она непрерывна и дифференцируема на
удовлетворяет условиям теоремы Ролля, она непрерывна и дифференцируема на  и равна нулю
и равна нулю 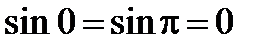 .
.
 ,
,
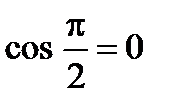 ,
,  .
.
Замечание. Если не выполнено условие дифференцируемости во внутренних точках  , то утверждение Ролля может быть неверным.
, то утверждение Ролля может быть неверным.
Пример.  непрерывна
непрерывна 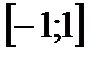 .
.  , однако,
, однако,  внутри данного сегмента. Это потому что в точке
внутри данного сегмента. Это потому что в точке 
 не существует. Нет касательной, параллельной оси
не существует. Нет касательной, параллельной оси  .
.






