1 Пусть 
. Так как 
сохраняет постоянное значение на всей числовой оси, то в произвольно выбранной точке 
любому приращению переменной 
соответствует приращение функции 
.
,
то есть
.
2 Пусть 
, где 
– натуральный показатель, – произвольная точка. Придадим приращение , тогда функция получит приращение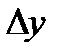 
:
.
,
следовательно,
.
3 Пусть задана показательная функция 
.
,
,
,
.
При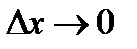 
, тогда имеем
,
.
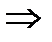
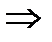
4 Производная логарифмической функции 
.
Возьмем любое значение 
из области определения и дадим ему приращение 
, тогда
.
,
,
здесь – 
и при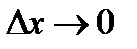 
.
Следовательно,
,
то есть
или
,
,
.
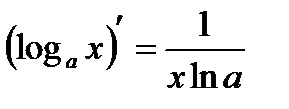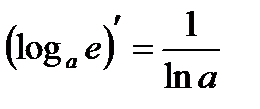5 Производная 
и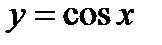 
.
Пусть – приращение произвольно выбранного значения аргумента функции .
,
,
.
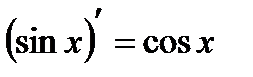Аналогично 
.
6 Пусть задана функция 
.
, 
.
7 Производная обратных тригонометрических функций
Пусть 
(рис. 3).
|
| Рисунок 3 – График функции
|
Рассмотрим обратную функцию 
. Эта функция в интервале 
монотонна. Её производная 
не равна нулю на этом интервале. Следовательно, 
, но 
. Так как 
в 
не равен нулю, следовательно, 
, то есть
.
Аналогично найдем 
. По определению функция должна удовлетворять условию , при этом 
монотонна.
,
следовательно,
.
Но 
. Тогда
или
;
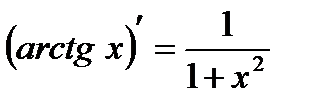(рис. 4);
.
|
Рисунок 4 – График функции 
|
8 Производные гиперболических функций
Пусть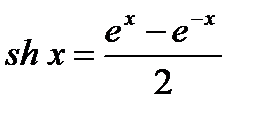 
, то
,
;
;
,
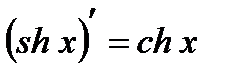то есть
;
.
9 Производная степенной функции с любым показателем
Пусть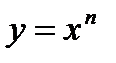 
, где 
– натуральное число.
.
Рассмотрим случай, когда 
.
–
это сложная функция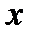 
, ее производная находится
.
Так как
,
то
.
Справедливо и для 
.
Сводная таблица формул дифференцирования
1. 
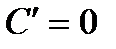, где 
– постоянная.
2. .
3. . 3’. .
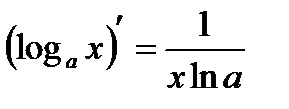4. . 4’. .
5. .
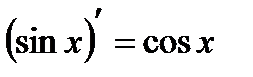6. .
7. .
8. .
9. .
10. .
11. .
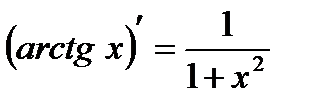12. .
13. .
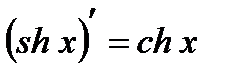14. .
15. .
16. .
