Теорема 1. Если функция 
и 
дифференцируема в данной точке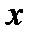 
, то в этой же точке дифференцируема и их сумма, причем производная суммы равна сумме производных от слагаемых:
.
Доказательство. Рассмотрим функцию 
.
,
.
Следовательно,
тогда
,
то есть , что и требовалось доказать.
Замечание. Теорема 1 справедлива для любого числа слагаемых.
Теорема 2. Если функции и дифференцируема в данной точке 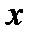, то в той же точке дифференцируемо и их произведение. При этом производная находится по следующей формуле:
.
Доказательство. Рассмотрим функцию 
, если 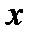получит приращение 
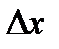, то функци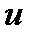и 
, 
и 
будут иметь соответственно приращения 
, 
и 
, причем
,
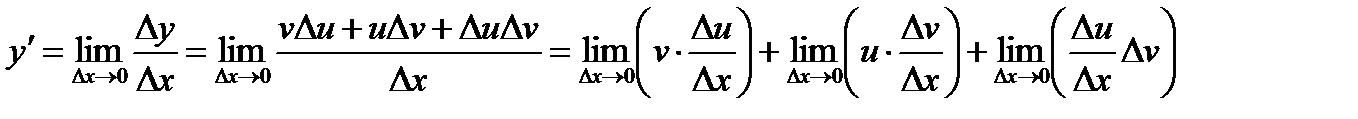так как при фиксированном 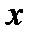и постоянны, то их можно вынести за знак предела
, 
, 
.
Следовательно,
,
что и требовалось доказать.
