1 Пусть дано уравнение 
.
Таким образом, для любой функции 
, заданной неявно имеет место тождество
,
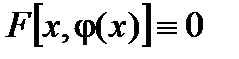справедливое для любого 
.
Пример. Найти производную функции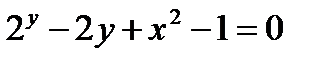 
.
Решение. Функция 
считается заданной неявно, если является тождеством относительно . При дифференцировани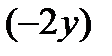и 
и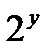 
следует рассматривать как сложные функции 
, а 
– промежуточный аргумент.
,
.
Производная неявной функции выражается как 
.
2 Параметрически заданная функция
(1)
где 
, любое значение 
соответствует 
и 
, когда 
изменяется в отрезке описывается некоторая линия.
Уравнения (1) называются параметрическими уравнениями кривой, – параметром.
Предположим, что 
имеет обратную функцию 
, следовательно, 
, таким образом (1) определяют 
, и говорят, от задана параметрически.
Выражение 
получится исключением из (1).
Параметрическое задание кривых широко используется в механике. Если в 
движется точка, и известны законы движения проекций этой точки на оси координат
(1’)
где параметр – время,
то (1’) – уравнение траектории точки.
Окружность:
.
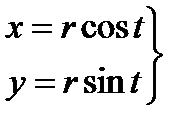
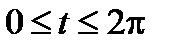Астроида:
.
Предположим, что 
и 
имеют производные. 
имеет обратную функцию 
, которая также имеет производную, следовательно, 
, заданную параметрически, можно рассматривать как сложную функцию.
,
– промежуточный аргумент.
,
,
.
Пример. Найти производную функции, заданной параметрически
Решение.
,
,
.
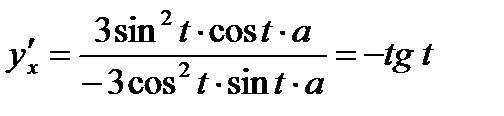