ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ
ОДНОЙ ПЕРЕМЕННОЙ
Конспект лекций
1 Производная функции, ее геометрический и механический смысл
1.1 Примеры, приводящие к понятию производной 
при неравномерном движении
дает среднюю скорость.
Пусть в некоторый момент времени точка занимает положение 
, а через 
– 
(рис. 1).
|
| Рисунок 1 – |
, 
, 
.
Мгновенная скорость, получится как
1.2 Процесс наполнения сосуда 
, зависимость наполненного сосуда от времени
,
.
Определение производной
Пусть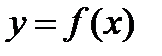 
. Аргумент 
получил приращение 
, следовательно, и функция 
получила приращение 
, то есть
.
,
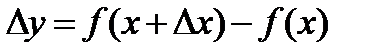тогда
,
.
Заметим, что для любой переменной производная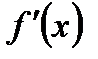 
имеет определенное значение, то есть производная является функцией от . Обозначение:
, 
, 
;
при 
или 
.
Операция нахождения производной называется дифференцированием этой функции.
Пример. Вычислить производную функции 
.
Решение. Пусть переменная получила приращение 
, то есть 
. Найдем приращение функции как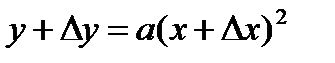 
, следовательно
,
;
.
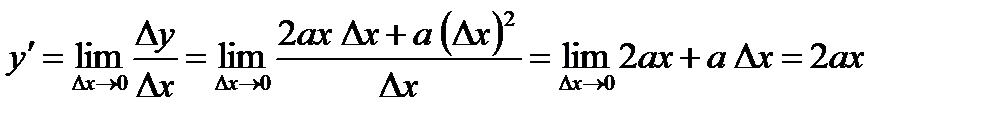Рассмотрим график функции 
(рис. 2).
|
| Рисунок 2 – |
Угловой коэффициент секущей 
:
.
Если 
, то секущая , поворачиваясь вокруг точки 
, в пределе переходит в касательную 
, так как касательная является предельным положением секущей, когда точки пересечения сливаются.
,
.
Геометрический смысл производной состоит в том, что она равна угловому коэффициенту касательной:
– уравнение касательной.
Подобным образом находится уравнение нормали к кривой, то есть перпендикуляр к касательной в точке касания имеет вид
.
Геометрический смысл производной дает возможность, если дан график, проследить за наклоном касательной к нему и сразу построить ориентировочный график производной.
Отметим, что если 
при некотором значении 
обращается в 
(при 
), то в соответствующей точке угловой коэффициент графика касательной равен , то есть касательная параллельна оси 
; если производная претерпевает скачок, то и касательная поворачивается скачком, то есть график имеет излом, если функция уходит в , то и производная уходит в .
