Рівняння
,
де 
є загальним рівнянням кривої другого порядку на координатній площині 
.
Очевидно, що отримані канонічні рівняння еліпса, гіперболи і параболи,, є частинними випадками рівняння. Але виникає питання, чи визначає це рівняння ще якісь лінії на координатній площині. Відповідь на нього дає наступна теорема.
Теорема. Для кожного рівняння існує система координат 
, в який воно набуває наступного вигляду:
1) 
‑ коло;
2) 
‑ еліпс;
3) 
‑ порожня множина точок (уявний еліпс);
4) 
‑ точка 
;
5) 
‑ гіпербола;
6) 
‑дві прямі що перетинаються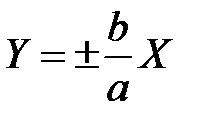 
;
7) 
, 
‑парабола;
8) 
або 
‑ дві паралельні прямі;
9) 
або 
‑ порожня множина точок;
10) 
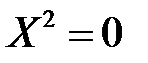або 
‑ вісь 
або 
.
Рівняння п.п.1-10 називаються канонічними виглядами рівняння. Способи побудови системи координат 
, в який рівняння набуває канонічного вигляду, покажемо на наступних прикладах.
Привести до канонічного вигляду рівняння кривої другого порядку:
1) 
Згрупуємо члени з 
та з 
та виділимо повні квадрати:
Застосуємо формули паралельного переносу:
,
де 
-центр нової системи координат.
У нашому впадку 
, тому набудуть вигляду:
Підставимо 
в отримане рівняння, тоді в системі 
отримаємо коло з радіусом 
:
2) 
Якщо в 
, то спершу слід застосувати формули повороту координатних осей
щоб при належному виборі кута 
звільнитися від члена з добутком координат.
Підставляючи 
та 
в задане рівняння, отримаємо:
Далі розкриємо дужки та приведемо подібні доданки:
Виберемо кут повороту 
так, щоб коефіцієт при 
в обернувся в нуль:
Обидві частини рівняння поділимо на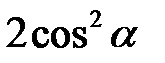 
. Слід зазначити, що 
, оскільки якщо це не так, то з рівняння випливає, що і 
. А це суперечить основній тригонометричній тотожності 
.
Після ділення отримаємо:
тобто 
.
Домовимось завжди брати для 
з двох можливих значень додатне, а кут повороту 
в першій чверті. Таким чином, з двох можливих значень обираємо 
.
Оскільки 
, а кут повороту знаходиться в першій чверті, то за відомим значенням 
функції 
та 
можуть бути визначено наступним чином:
.
В нашому випадку: 
.
При цих значеннях рівняння набуває вигляду:
.
Згрупувавши члени з 
та 
і виділивши повні квадрати, маємо:
.
.
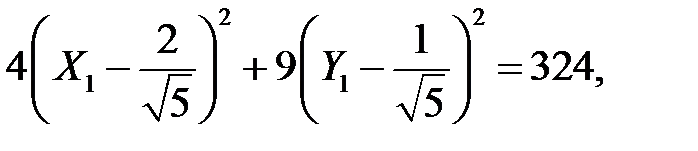
Виконавши паралельне перенесення системи координат в т. 
за формулами, отримаємо:
.
Останнє рівняння є рівнянням еліпса (Рис. 44.1).
Рис. 44.1
3) 
Виділимо відносно 
повний квадрат:
або в центрі 
‑ уявний еліпс.
4) 
Здійснивши аналогічні попереднім перетворення, отримаємо
‑ точка 
в системі 
‑ точка 
в системі 
.
5) 
.
Так як 
, то спершу застосуємо формули повороту координатних осей, щоб при належному виборі кута 
звільнитися від члена з добутком координат.
Після підстановки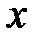 
та 
в задане рівняння, отримаємо:
Далі розкриємо дужки та приведемо подібні доданки:
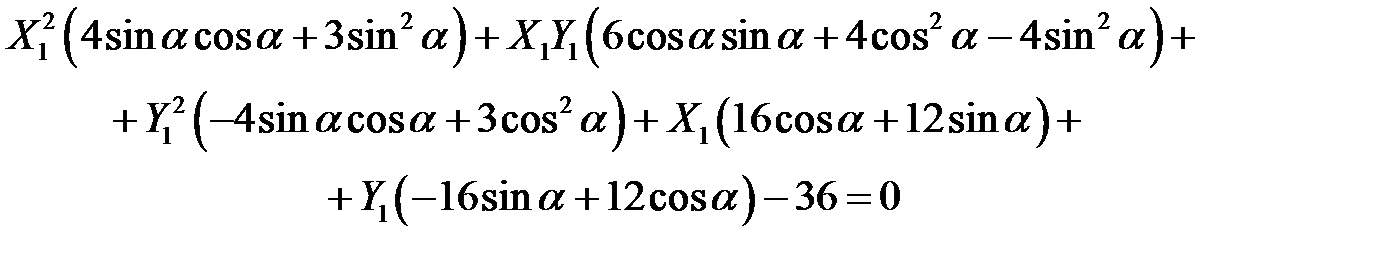
Виберемо кут повороту 
так, щоб коефіцієт при 
в обернувся в нуль:
Обидві частини рівняння поділимо на 
, 
. Після ділення отримаємо:
тобто 
.
Домовимось завжди брати для 
з двох можливих значень додатне, а кут повороту 
в першій чверті. Таким чином, з двох можливих значень обираємо 
.
Оскільки 
, а кут повороту знаходиться в першій чверті, то за формулами
.
При цих значеннях рівняння набуває вигляду:
.
Згрупувавши члени з 
та 
і виділивши повні квадрати, маємо:
.
.
Виконавши паралельне перенесення системи координат в т.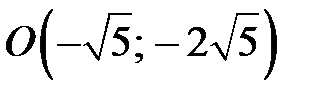 
за формулами, отримаємо:
,
отже, рівняння набуде вигляду:
.
Отримане рівняння є канонічним рівнянням гіперболи (Рис. 44.2).
Рис. 44.2
6) 
Згрупуємо доданки відносно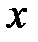 
та 
і виділимо повні квадрати:
Центр нової системи координат перенесемо в точку 
. В новій системі координат 
маємо рівняння
,
що визначає дві прямі 
7) 
Застосуємо формули повороту координатних осей, щоб при належному виборі кута 
звільнитися від члена з добутком координат та підставимо 
та 
в задане рівняння:
або
Прирівнюючи до нуля коефіцієнт при добутку 
отримаємо:
,
звідки
,
тобто
.
Візьмемо 
, звідки 
. Тоді
.
При цих значеннях рівняння набуває вигляду:
.
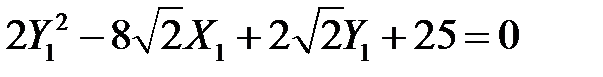Згрупувавши члени з 
та 
і виділивши повні квадрати, маємо:
;
Виконавши паралельне перенесення системи координат в т. 
за формулами, маємо:
Відносно нової системи з центром в точці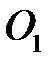 
отримали канонічне рівняння параболи, симетричної відносно осі 
(Рис. 44.3):
.
Рис. 44.3
8) 
.
Виділимо повний квадрат:
або 
, тобто 
.
В результаті отримали дві паралельні прямі: 
та 
.
9) 
.
Виділяючи повний квадрат, одержимо 
. Ца рівняння не має дійсних розв’язків, тому визначає порожню множину точок.
10) 
, звідки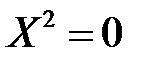 
. Це рівняння визначає вісь 
.
Задачі для самостійної роботи
Привести до канонічного вигляду рівняння кривих другого порядку:
1) 
;
2) 
;
3) 
;
4) 
;
5) 
;
6) 
;
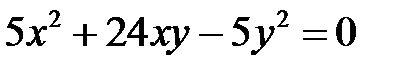7) 
;
8) 
;
9) 
;
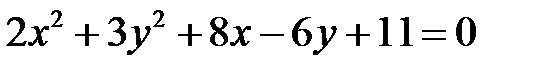10) 
.
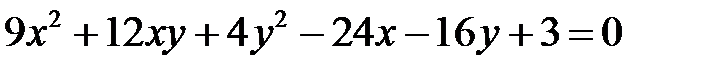