Нехай задана плоска лінія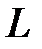 
і точка 
, що не знаходиться з цією лінією у одній площині. Поверхня, яка утворюється прямими, що проходять через кожну точку заданої лінії 
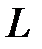і задану точку 
, називається конічною поверхнею, або конусом (Рис. 46.1). Лінія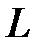 
- називається напрямною конуса, точка 
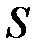- вершиною конуса, а лінії, що проходять через точку напрямної і вершину, називаються твірними.
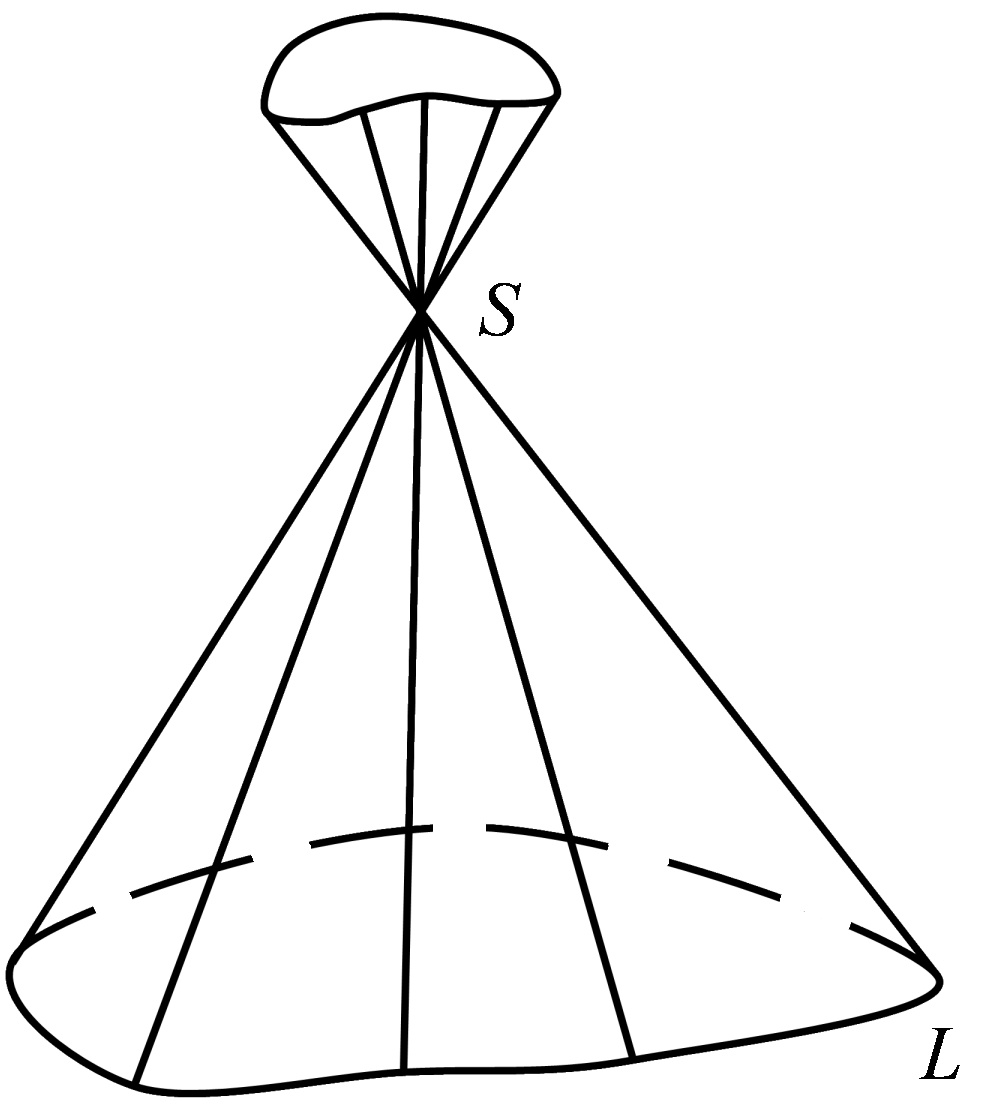
Рис. 46.1
Візьмемо у якості напрямної коло радіуса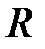 
, що знаходиться у площині 
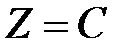з центром в точці 
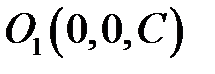на осі 
(Рис.46.2).
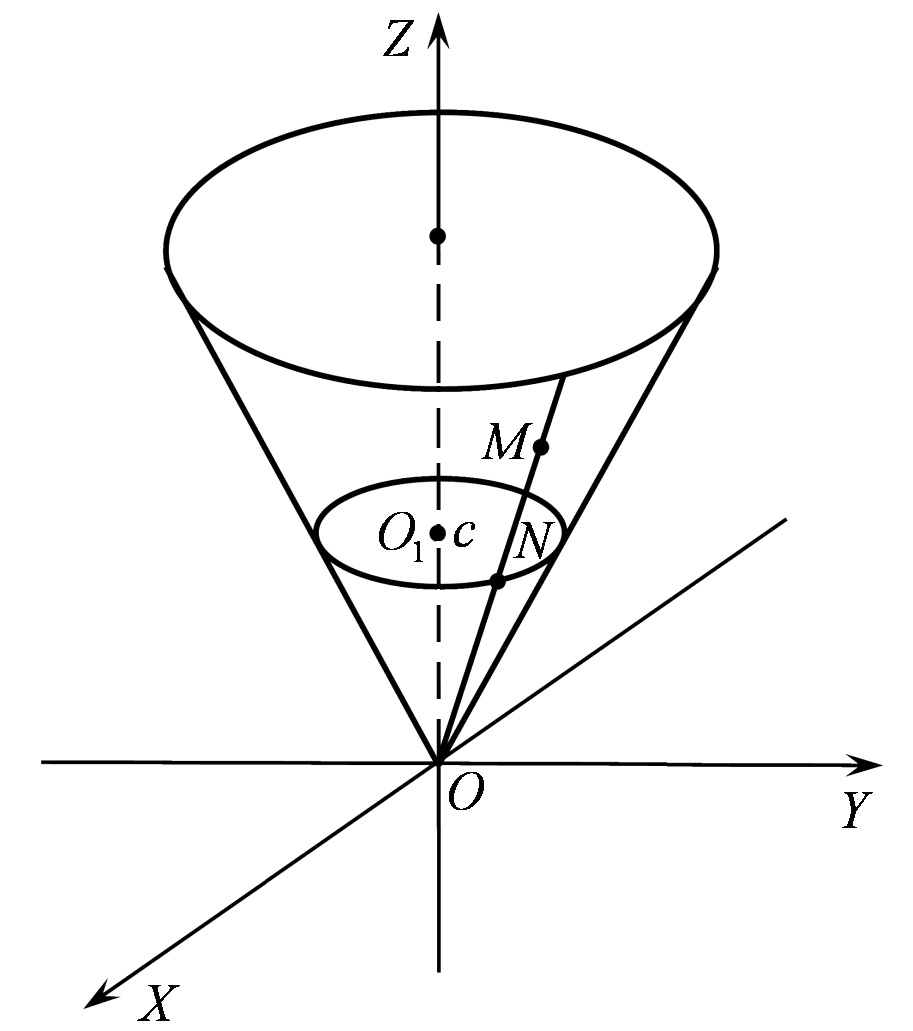
Рис. 46.2
Таке коло у системі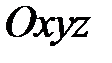 
визначається системою рівнянь
Припускаємо, що точка 
- вершина конуса. Нехай 
- довільна точка на конусі. Проведемо твірну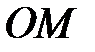 
, яка перетне коло, що є напрямним, у точці 
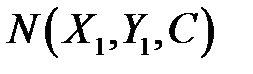. Оскільки точка 
належить до кола, то її координати задовольняють, зокрема виконується рівність:
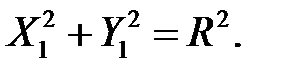
Вектори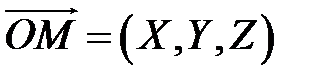 
і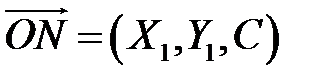 
- колінеарні, тому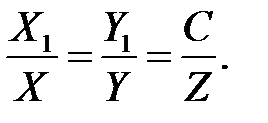 
З останньої рівності знаходимо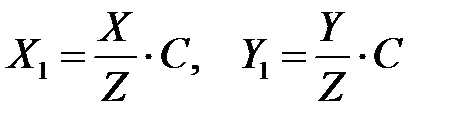 
і підставляємо у:
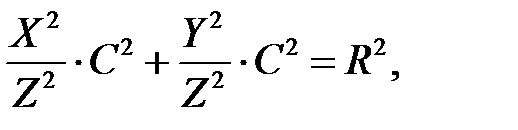
або
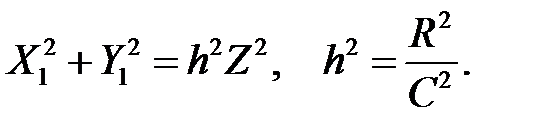
Останнє рівняння і визначає розглянутий конус.
