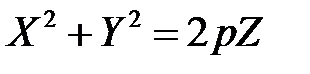Поверхнею обертання називається поверхня, утворена обертанням плоскої лінії навколо прямої, що знаходиться у тій же самій площині. Пряма, навколо якої відбувається обертання, називається віссю обертання.
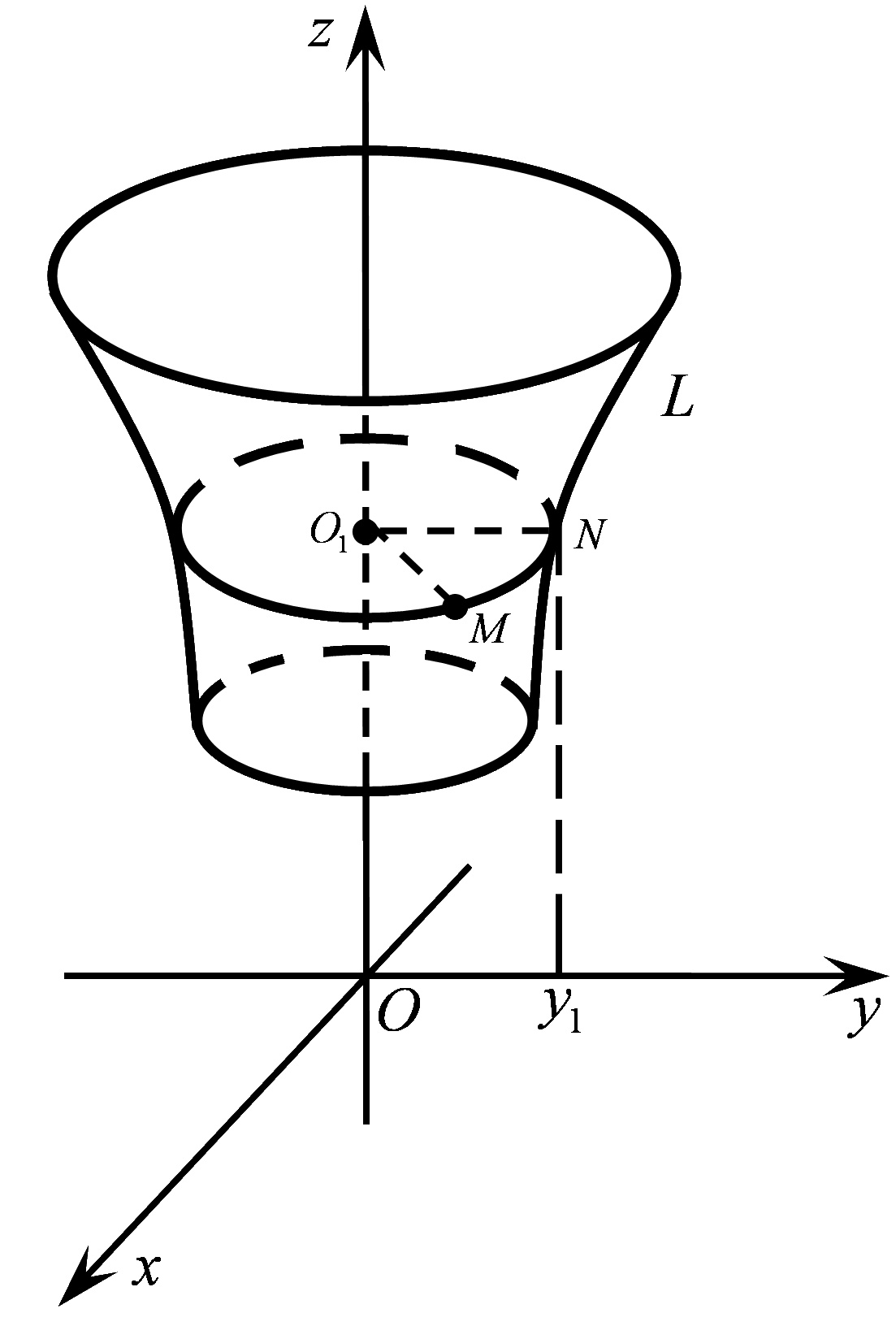
Рис. 47.1
Розглянемо криву 
, яка в системі координат 
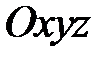знаходиться у площині 
і задається рівнянням
Знайдемо рівняння поверхні, що утворюється обертанням цієї кривої навколо осі 
(Рис.47.1). Розглянемо довільну точку поверхні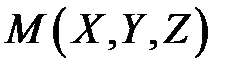 
. Через цю точку проведемо площину, перпендикулярну до осі 
. Нехай 
- точка перетину цієї площини з віссю 
, а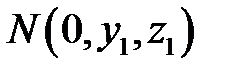 
- точка перетину з кривою 
. Тоді 
, а 
. Але 
, як радіуси одного кола. Отже, координати точки 
дорівнюють 
і оскільки точка 
належить кривій 
, то мають задовольняти рівняння:
Таким чином, є рівнянням розглянутої поверхні обертання. Аналогічно отримується рівняння поверхні, що утворюється обертанням кривої навколо осі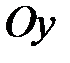 
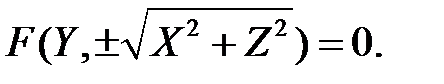
Коли лінія знаходиться у площині 
і її рівняння
то рівняння поверхні, утвореної обертанням цієї лінії навколо осі 
має вигляд:
Розглянемо поверхні, що утворюються при обертанні кривих другого порядку, заданих канонічними рівняннями.
1. Еліпсоїд обертання.
Нехай еліпс, що знаходиться у площині 
, задається рівнянням
і обертається навколо осі 
(Рис. 47.2)
Рис. 47.2
Утворена при цьому поверхня називається еліпсоїдом обертання і має рівняння (див.)
2. Однопорожнинний гіперболоїд обертання
Візьмемо у площині 
гіперболу
і здійснимо її обертання навколо осі 
(Рис. 47.3)
Рис. 47.3
Утворена при цьому поверхня називається однопорожнинним гіперболоїдом обертання і має рівняння
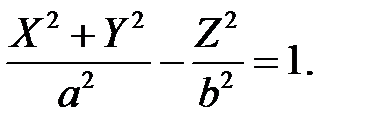
3. Двопорожнинний гіперболоїд обертання
Якщо цю саму гіперболу обертати навколо осі 
, то отримаємо поверхню, яка називається двопорожнинним гіперболоїдом обертання (Рис. 47.4) і згідно з визначається рівнянням
або 
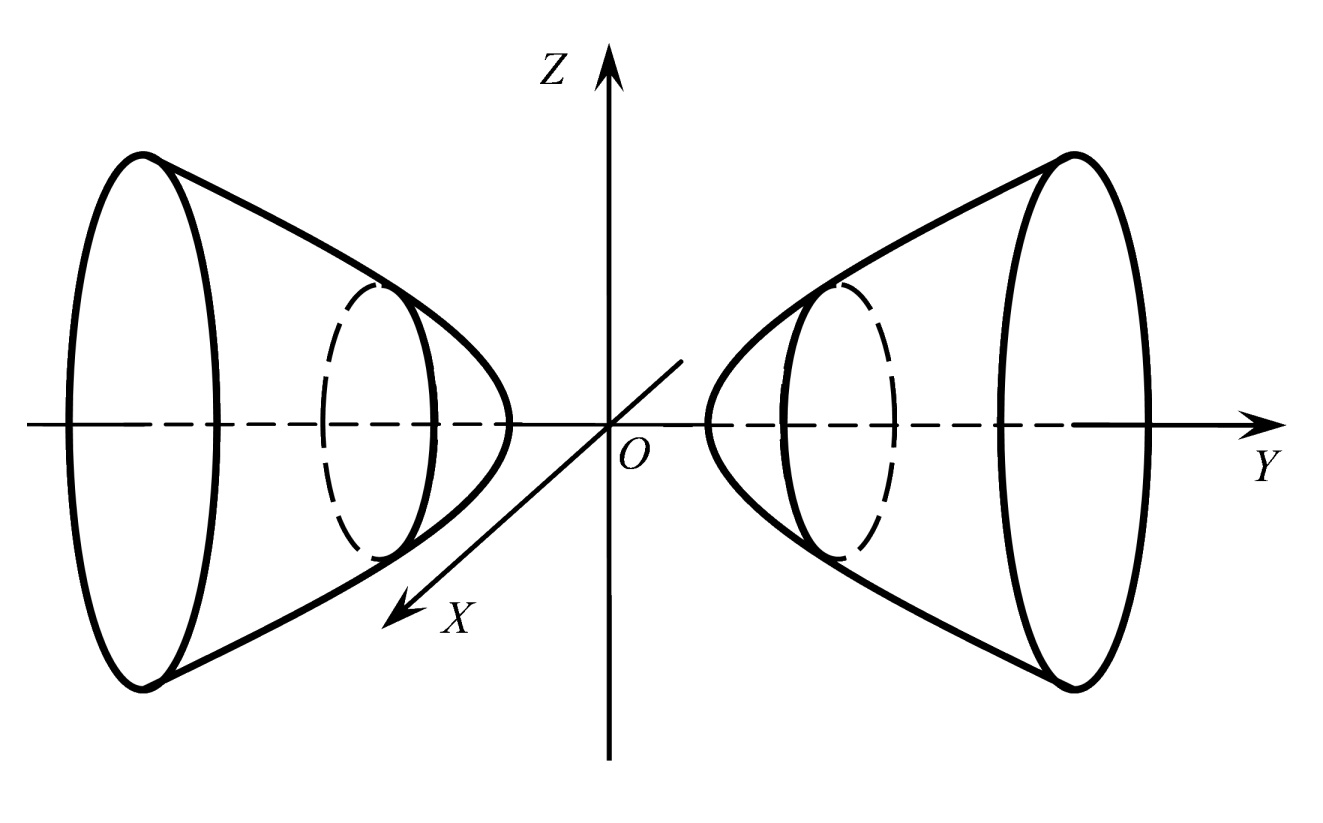
Рис. 47.4
4. Параболоїд обертання.
Нехай парабола
Рис. 47.5
обертається навколо осі 
(Рис. 47.5). Утворена поверхня називається параболоїдом обертання і визначається рівнянням
