Гіперболою називається множина точок площини, модуль різниці відстаней від кожної з яких до двох заданих точок, які називаються фокусами, є величина стала.
Нехай точки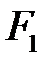 
і 
- це фокуси гіперболи. Для виведення її рівняння система координат обирається так само, як і у випадку еліпса (Рис. 40.1). Відрізки, що з’єднують довільну точку гіперболи 
з фокусами, називаються її фокальними радіусами (Рис. 40.1) і знаходяться за формулами. Згідно визначення гіперболи модуль різниці фокальних радіусів для точок гіперболи – це стала величина, яку позначимо 
. З властивостей сторін трикутника 
, 
. Тоді має виконуватись рівність:
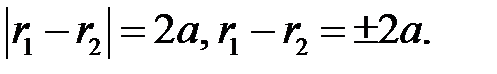
Після підстановки у фокальних радіусів з отримаємо:
Внаслідок перетворень останнього рівняння, аналогічно проведеним у випадку еліпса, приходимо до наступного:
Рівняння називається канонічним рівнянням гіперболи. Як і еліпс, гіпербола є кривою другого порядку.
Встановимо основні властивості гіперболи.
1. З можна бачити що 
, тобто 
Це означає, що гіпербола - необмежена лінія, яка складається з двох частин, що розміщуються у частинах координатної площини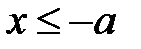 
та 
.Ці частини гіперболи називаються її гілками.
2. Як і еліпс, гіпербола симетрична відносно осей 
і 
і точки 
Таким чином, гіпербола - це теж центральна крива.
Точки 
є точками перетину гіперболи з віссю 
і називаються її вершинами. З віссю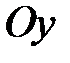 
гіпербола не перетинається.
Відрізок 
називається дійсною віссю гіперболи, а відрізок 
називається її уявною віссю.
3. Асимптоти гіперболи.
Здійснимо над рівнянням наступне перетворення:
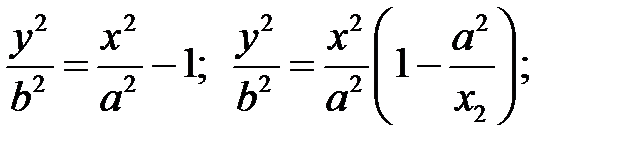
Ця рівність означає, що для будь-якої точки гіперболи виконується нерівність
, або 
Нерівності означають, що точки гіпербли знаходяться у частині координатної площини, обмеженої прямими
Розглянемо величину 
. Тоді з можно записати:
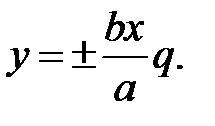
Величина 
лежить у межах 
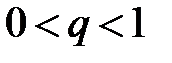і прямує до 
,коли 
прямує до нескінченності. Це означає, що при прямуванні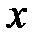 
до нескінченності точки гіперболи і точки прямих необмежено зближуються. Прямі називаються асимптотами гіперболи. Вони є діагоналями прямокутника, що утворюють прямі 
і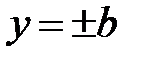 
. Він називається основним прямокутником гіперболи.
Встановлені властивості дають можливість зобразити гіперболу (Рис. 41.1).
4. Ексцентриситет гіперболи і формули для фокальних радіусів.
Ексцентриситетом гіперболи називається відношення відстані між фокусами до довжини дійсної осі:
Рис. 41.1
З знаходимо
З останньої формули можна бачити, що ексцентриситет гіперболи характеризує форму її основного прямокутника, а значить і форму гіперболи.
Окрім того, поняття ексецентриситета дає можливість знайти прості формули для фокальних радіусів точки на гіперболі:
Виведення цих формул здійснено аналогічно виведенню формул для еліпса.
5. Директриси гіперболи.
Директрисами гіперболи називаються прямі, що визначаються рівняннями
Директриси гіперболи мають властивості, аналогічні до директрис еліпса. Якщо 
і 
- відстані від точки гіперболи до директрис (Рис. 41.1), то завжди виконується рівність
Таким чином, відношення фокального радіуса точки гіперболи до відстані від неї до відповідної директриси дорівнює ексцентриситету гіперболи.
