Нехай у просторі є деяка плоска лінія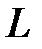 
і заданий ненульовий вектор 
.
Поверхня, утворена прямими, що проходять через кожну точку лінії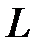 
паралельно до заданого вектора 
, називається циліндричною поверхнею (Рис. 45.1).
Прямі, що утворюють циліндричну поверхню, називаються твірними, а лінія 
називається напрямною.
Складемо рівняння циліндричної поверхні за умов, що напрямною є крива, що міститься у площині 
, а вектор 
- орту осі 
.
Тоді напрямна задається рівнянням
а твірні паралельні осі 
(Рис. 45.2).
| 
|
| Рис. 45.1 | Рис. 45.2 |
Візьмемо 
- довільну точку циліндричної поверхні. Проведемо через цю точку твірну до перетину з напрямною у точці 
. Оскільки ця точка належить до напрямної, то її координати мають задовольняти рівняння. Отже, для будь якої точки на циліндрі координати 
задовольняють першому рівнянню системи, а третя координата 
може бути довільною:
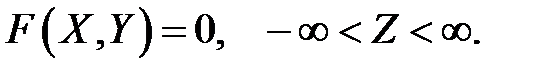
Рівняння і є рівнянням циліндричної поверхні, що зображена на Рис. 45.2.
Якщо у якості напрямної взяти еліпс, то з отримаємо рівняння еліптичного циліндра:
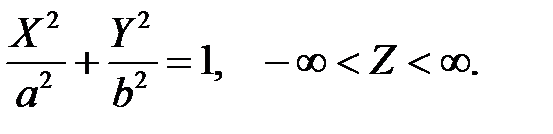
Якщо 
, то еліпс є колом і з знаходимо рівняння кругового циліндра:
