Для правої гілки гіперболи фокальні радіуси визначаються за формулами
.
Отже, за умовою задачі маємо рівняння
,
звідки
.
З канонічного рівняння гіперболи маємо, що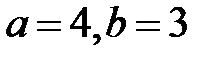 
, тоді 
і 
. Тобто 
.
Ординату шуканої точки знайдемо з рівняння гіперболи:
.
Таким чином, умові задачі задовольняють дві точки: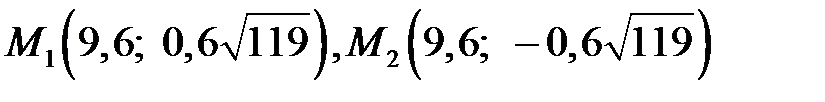 
.
Задачі для самостійної роботи
1. Гіпербола, симетрична відносно осей координат, проходить через точки 
. Записати її канонічне рівняння та побудувати гіперболу.
2. Скласти канонічне рівняння, побудувати параболу та її фокус, якщо відомо рівняння директриси: 
.
3. На гіперболі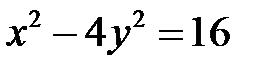 
взято точку з ординатою, рівною 1. Знайти відстані від цієї точки до фокусів.
4. Еліпс, симетричний відносно осей координат, проходить через точку 
та має ексцентриситет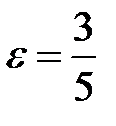 
. Записати його канонічне рівняння.
5. Знайти рівняння і побудувати гіперболу, фокуси якої розташовані на осі абсцис симетрично відносно початку координат, якщо відстань між її директрисами дорівнює 
, а ексцентриситет 
.
6. Кут між асимптотами гіперболи дорівнює 
. Обчислити її ексцентриситет.
7. Ордината точки на параболі 
дорівнює 5. Знайти відстань від цієї точки до фокуса. Побудувати параболу, її фокус і директрису.
8. На параболі 
знайти точку, відстань до якої від директриси дорівнює 4.
9. Скласти рівняння і побудувати еліпс, симетричний відносно осей координат, якщо йому належить точка 
і відстань між фокусами дорівнює 8.
10. Скласти рівняння і побудувати гіперболу, якщо її ексцентриситет 
, а фокуси співпадають з фокусами еліпса 
.
Питання для повторення
1) Еліпс. Означення, канонічне рівняння та дослідження форми.
2) Гіпербола. Означення, канонічне рівняння та дослідження форми.
3) Парабола. Означення, канонічне рівняння та дослідження форми.
