Еліпсом називається множина усіх точок площини, для яких сума відстаней від кожної до двох заданих точок, які називаються фокусами, є сталою величиною. Нехай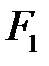 
і 
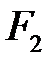- фокуси еліпса. Для виведення рівняння еліпса система координат обирається, так щоб фокуси знаходились на осі 
, а початкова точка співпадала з серединою відрізка 
. Осі координат спрямовуються так, щоб система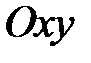 
була правою. (Рис. 40.1)
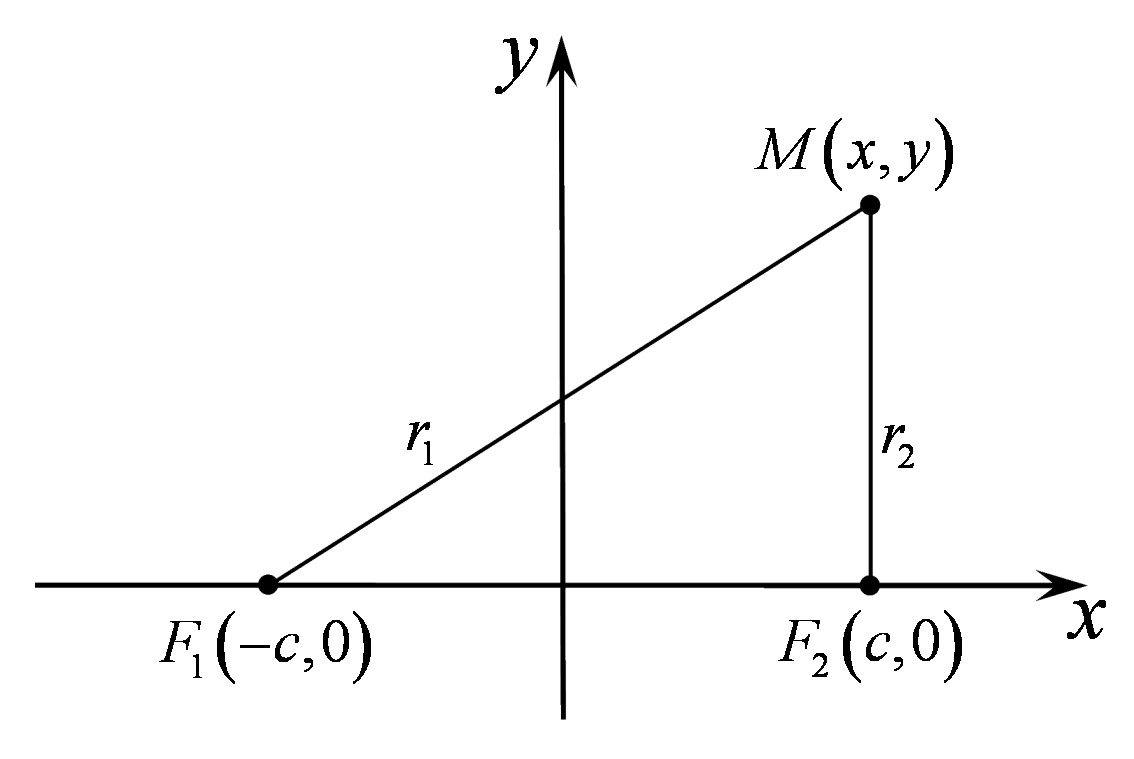
Рис. 40.1
Нехай в обраній системі координат фокуси мають координати 
, 
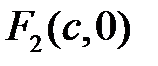. Візьмемо довільну точку еліпса 
. Відрізки, що з’єднують точку еліпса з фокусами, називаються фокальними радіусами точки. Позначимо їх 
, 
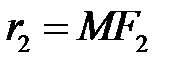. Згідно визначення для будь-якої точки на еліпсі сума фокальних радіусів стала величина, яку позначимо 
:
.
Причому за властивостями сторін трикутника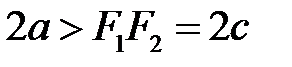 
, отже, 
.
Фокальні радіуси дорівнюють
, 
.
Підставимо у
і отриману рівність перетворимо до вигляду:
.
Далі обидві частини останньої рівності підносимо до квадрату і спрощуємо:
,
,
.
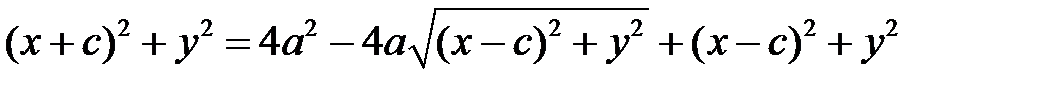Знову підносимо обидві частини рівності до квадрату:
,
,
.
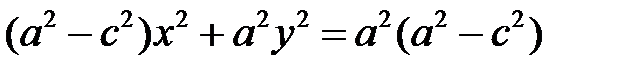Оскільки 
, то введемо позначення 
і знайдемо з останнього
.
Після ділення на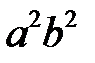 
обох частин остаточно знаходимо
Рівняння називається канонічним рівнянням еліпса.
У рівняння координати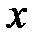 
і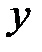 
входять у другій степені, тому кажуть, що еліпс – крива другого порядку.
Виведене рівняння дозволяє встановити наступні властивості еліпса.
1. Обмеженість еліпса. З рівняння випливає 
або 
, 
чи 
, 
. Геометрично ці нерівності означають, що еліпс – це обмежена лінія, яка знаходиться у прямокутнику, утвореному прямими 
.
2. Симетричність і точки перетину з координатними осями. Оскільки координати 
і 
входять у тільки у квадраті, то з того, що точка 
належить еліпсу, випливає, що і точки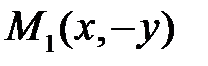 
, 
, 
належать цьому еліпсу. Це означає, що осі 
і 
є осями симетрії еліпса, а точка 
- його центром. Оскільки еліпс має центр симетрії, то він є центральною кривою.
При 
з маємо 
. Отже, точки 
, 
є точками перетину еліпса з віссю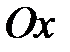 
. Якщо 
, то 
, 
і точки 
і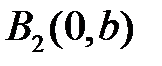 
є точками перетину еліпса з віссю 
(Рис. 40.2). Точки перетину еліпса з осями координат називаються його вершинами. Відрізок 
називається великою віссю еліпса, а відрізки 
великими півосями. Відрізок 
називається малою віссю еліпса, а відрізки 
його малими півосями.
Рис. 40.2
3. Ексцентриситет еліпса. Обчислення фокальних радіусів точки на еліпсі.
Ексцентриситетом еліпса називається відношення відстані між фокусами до довжини великої осі:
або, оскільки 
,
Можна бачити, що ексцентриситет може приймати значення 
. З випливає,що чим більше ексцентриситет, тим менше мала вісь за велику і тим більше витягнутий еліпс вздовж великої осі. У граничному випадку 
маємо 
і еліпс перетворюється у відрізок 
. При 
, 
, тобто фокуси еліпса співпадають, а сам він перетворюється у коло радіуса 
. Це коло, як випливає з, визначається рівнянням 
.
За допомогою ексцентриситету можна знайти прості вирази для фокальних радіусів точки на еліпсі. Дійсно, з знаходимо
і підставляємо у формули для фокальних радіусів (11.2):
.
Враховано, що завжди 
.
Після аналогічних перетворень для другого фокального радіуса знаходимо остаточно
.
4. Директриси еліпса і їх властивості.
Прямі (Рис. 40.2)
називаються директрисами еліпса. Головною властивістю директис є наступна: відношення фокального радіуса точки еліпса до відстані від неї до відповідної директриси дорівнює ексцентриситету еліпса. Тобто, якщо 
(Рис. 40.2), то
.
Дійсно,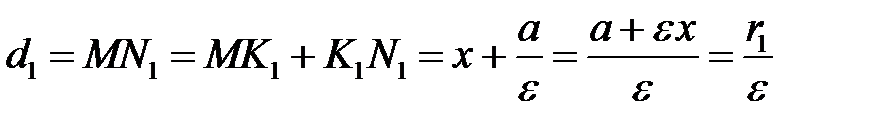 
,
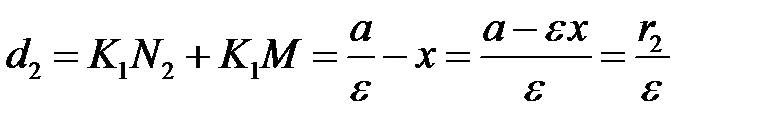. Звідси випливають рівності.
