Разложение некоторых элементарных ф-ций в ряде Маклорена

Разложение функции f(x)=e^x в ряд Маклорена:

f(x)=f′(x)=f″(x)=…=f⁽ⁿ⁾(x)=…=e^x.

f(0)=f′(0)=f″(0)=…=f⁽ⁿ⁾(0)=…= 1.

Составим для функции f(x)=e^x формально ряд Маклорена:

1+ .

Найдём области сходимости этого ряда.

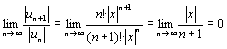при любых x, следовательно, областью сходимости ряда является промежуток (-∞;+∞). Заметим, что так как ряд сходится абсолютно, то при любых х и тем более 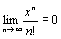при любых х. Так как f⁽ⁿ⁺¹⁾(x)=e^x и f⁽ⁿ⁺¹⁾(с)=e^с, то =e^c =0. Таким образом, имеет место разложение при x (-∞;+∞)

e^x =1+

64) Применение рядов к приближенным вычислениям значений ф-ции, определённых интегралов

Eсли подинтегральная функция раскладывается в степенной ряд, а пределы интегрирования принадлежат интервалу сходимости этого ряда, то возможно приближенное вычисление интеграла с наперед заданной точностью.

Вычислить интеграл с точностью до 0,001.

Решение.

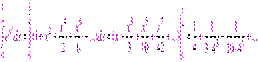
Проверим, можем ли мы отбросить остаток после второго члена полученного ряда.

.

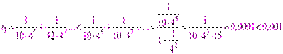Следовательно, .