ОБЪЕМ ТЕЛА: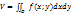 
ПЛОЩАДЬ ПЛОСКОЙ ФИГУРЫ: 
МАССА ПЛОСКОЙ ФИГУРЫ: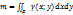 
. γ = γ(x;y) — плотность
СТАТИСТИЧЕСКИЕ МОМЕНТЫ: 
и 
МОМЕНТЫ ИНЕРЦИИ ПЛ. ФИГУРЫ: 
и 
МАССА ПЛОСКОЙ ПЛАСТИНКИ: γ = γ(x;y) — поверхностная плотность — непрер. ф-ция координат т. (x;y). Разобьем пластинку D на n Di, обозначим их площади через ∆Si, возьмем Mi(xi;yi) и найдем плотность в ней. Плотность в каждой т. Di const, найдем mi ≈ γ(x;y)∆Si. Т. к. m = ∑ mi, m ≈ ∑ γ(x;y)∆Si. n→∞ и max di→0. 
Приложение кри-1 рода
Длина кривой: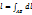 
Площадь цилиндрической поверхности: 
Масса кривой: 
Статические моменты:
Условия независимости КРИ-2 от пути интегрирования. Потенциал
Для того чтобы криволинейныйинт. 
не зависел от пути интегрирования в односвязной области D, в которой функции 
непрерывны вместе со своими частными производными, необходимо и достаточно, чтобы в каждой точке этой области выполнялось условие: 
