Теорема. Если степенной ряд 
сходится при x = x1, то он сходится и притом абсолютно для всех 
.
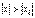Свойства степенных рядов
1. Сумма S(x) степенного ряда
Является непрерывной функцией в интервале сходимости (-R;R)
2. Степенные ряды 
,имеющие радиусы сходимости соотв-о 
, можно почленно складывать, вычитать и умножать. Радиус сходимости произведения, суммы и разности рядом не меньше чем меньшее из чисел
3. Степенной ряд внутри интервала сходимости можно почленно дифференцировать; при этом для ряда 
(пиши вместо скобки просто x)
При -R 
выполняется равенство
4. Степенной ряд можно почленно интегрировать на каждом отрезке, расположенном внутри интервала сходимости; при этом для ряда
(пиши вместо скобки просто x) при -R 
