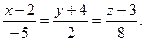Рівняння прямої в просторі, що проходить через дві задані точки

 

За двома точками 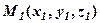і можна не тільки геометрично провести пряму лінію, але й скласти її рівняння. Для цього за напрямний вектор візьмемо , тоді за формулою (25) маємо

 

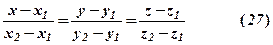
– рівняння прямої в просторі, що проходить через дві задані точки.

Приклад. Скласти рівняння прямої 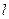, яка проходить через дві точки М₁(-1,2,3) і М₂(5,-2,1). Перевірити чи лежать на цій прямій точки М₃(-7,6,5), М₄(2,0,1), М₅(-4,4,4)?

Відповідь: так, ні, так.

 

3.16. Загальне рівняння прямої; перехід до канонічного рівняння

 

Пряма може бути задана двома площинами, що перетинаються по цій прямій. Нехай відомі їх рівняння

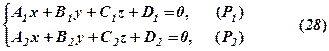
тоді система (28) називається загальними рівняннями прямої.

Щоб перейти до канонічних рівняннь вигляду (25), необхідно знайти вектор 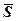і точку 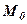цієї прямої.

Точку 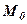знаходимо, як один із розв’язків системи (28). Наприклад, поклавши в (28) 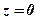знаходимо 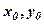, тоді і точку 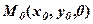. Напрямний вектор 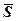, який є паралельним до кожної з площин і 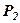, є перпендикулярним до їх нормальних векторів і , тобто 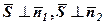(див. рис. 22). Тому вектор 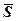можна знайти за допомогою векторного добутку 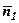і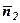

Знайдені координати 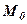і 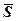підставляємо в канонічне рівняння (25).

Наприклад, від загальних рівняннь прямої

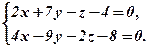
перейдемо до канонічних, поклавши в системі 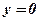(при ньому відносно більші коефіцієнти), знайдемо .

Нормальні вектори 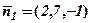і 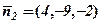. Тоді напрямний вектор

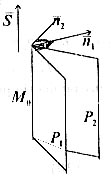
Рис. 22.

,

і канонічні рівняння набудуть вигляду:

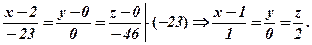
Приклад. Звести до канонічного вигляду загальне рівняння

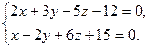
Відповідь: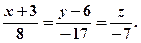

3.17. Кут між двома прямими в просторі. Умова паралельності та перпендикулярності прямих

Кут 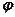між прямими

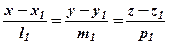і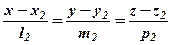

дорівнює кутові між їх напрямними векторами 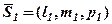і 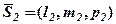, тому

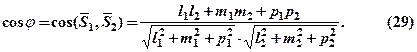
Умови паралельності і перпендикулярності прямих відповідно запишуться

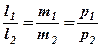і

Приклад. Знайти гострий кут між прямими

 

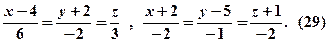
Розв’язання. За формулою (29) отримуємо

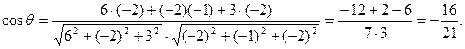Оскільки 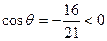, то кут q тупий, , а гострий кут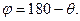

Відповідь:

Приклад 2. Скласти рівняння прямої 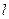, яка проходить через точку М(2,-4,3) і паралельна прямій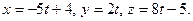

Розв’язання. Від параметричного рівняння переходимо до канонічного 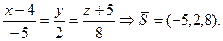За умовою паралельності прямих , тобто напрямним вектором нової прямої може служити відомий вектор 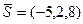і за формулою (25) маємо