3.15. Канонічне та параметричне рівняння прямої в просторі
Аналогічна задача вже розв’язувалась для прямої на площині. Отже, необхідно скласти рівняння прямої 
, що проходить через дану точку 
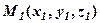паралельно напрямному вектору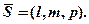 
Нехай, 
– довільна точка прямої, тоді вектори 
і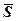 
колінеарні, а це значить, що координати їх пропорційні, тому отримуємо
– канонічні рівняння прямої. Прирівнюючи кожний з дробів (25) до параметра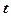 
, запишемо параметричні рівняння прямої
Приклад. За точкою М(1,5,2) і напрямним вектором 
необхідно: 1) скласти канонічне рівняння прямої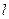 
; 2) побудувати цю пряму.
Розв’язання. 1) За формулою (25) запишемо канонічне рівняння прямої :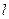
2) Розглянемо два способи побудови прямої .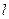
Перший спосіб. В системі координат XYZ будуємо вектор 
і точку М(1,5,2) і проводимо через точку М пряму паралельну вектору 
Другий спосіб. За формулою (26) записуємо рівняння прямої 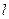в параметричному вигляді:
При довільних значеннях t із системи знаходимо координати відповідних точок, які належать прямій 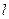. Так при t=1 знаходимо координати М1(4,5,6). Через дві точки М і М1 проводимо пряму 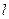(див. Мал.)
