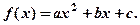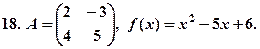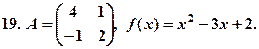Приклад 4.
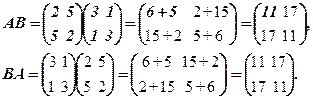
Легко перевірити, що довільна квадратна і одинична матриці комутативні, і при цьому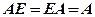 
.
Приклад 5. Перевірити останню рівність, якщо
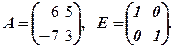
Можна показати, що множення матриць має такі властивості:
де 
– число;
.
Тут мається на увазі, що всі записані добутки матриць існують.
Приклад 6. Перевірити властивості 1-4, якщо число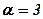 
, а матриці 
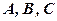такі:
, 
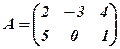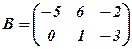, С= 
.
Розглянемо поняття степеня квадратної матриці.
Означення 3. Квадратом матриці 
(позначається 
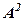) називається добуток 
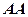, тобто 
.
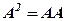Аналогічно вводиться 
.
Приклад 7. Для матриць 
і 
, де
, 
,
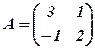довести, що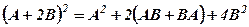 
, та знайти значення виразів.
Означення 4. Якщо 
- заданий многочлен і деяка квадратна матриця, то вираз
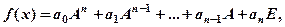
де 
- одинична матриця, називається многочленною матрицею.
Приклад 8. Для матриці
Знайти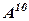 
Обчислити степені квадратних матриць:
9.. 10. 11..
12.. 13.. 14..
Перемножити прямокутні матриці:
15.. 16..
17..
Знайти 
, якщо задана матриця і функція 
