Іноді в роботі з таблицями (матрицями) прикладів типу 1–3 із 1.8., доводиться виконувати над ними певні операції. Так, якщо в прикладі 1 потрібно підрахувати заплановий розмір стипендій за семестр (6 місяців), то очевидно необхідно кожний елемент цієї матриці помножити на 6. Виникає необхідність множити матрицю на число.
Якщо в умовах прикладу 2 ми маємо відомості 3-х місяців одного квартала, то можна скласти зведену відомість за квартал, додаючи розміщені у відповідних графах дані стосовно кожного робітника.
Приходимо до дії додавання матриць.
Якщо в умовах прикладу 3, 1.8. позначити через 
і 
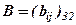– результати роботи 3-х змін за першу і другу добу відповідно, то можна знайти сумарні результати за дві доби додаванням відповідних елементів і позначити це
Отже з прикладів бачимо, що цілком природно виникає необхідність дій множення матриці на число і додавання матриць.
Означення 1. Добутком числа 
на матрицю 
розміру 
називається нова матриця 
того ж розміру, кожний елемент якої дорівнює відповідному елементу матриці 
помноженному на число , тобто
Матриця (–1) – протилежна матриці , і позначається 
.
Дія додавання вводиться тільки для матриць одного і того ж розміру.
Означення 2. Сумою двох матриць і розміру називається матриця 
того ж розміру, кожний елемент якої дорівнює сумі відповідних елементів матриць–доданків, тобто 
, і позначається 
.
Якщо ж 
, то 
— різниця матриць.
Дії додавання, віднімання і множення матриць на число називаються лінійними діями над матрицями.
Можна перевірити, що вони мають такі властивості:
Тут позначено через 0 – нульову матрицю і 
— протилежну матриці .
Вправа. Перевірити властивості 1–8 для матриць
і чисел 
.
Приклад. Задані матриці
, 
.
Знайти 1) 
; 2) 
.
Розв’язання. 1) 
.
2) 
.
