Мгновенная поставка, возникновение дефицита не допускается

Этот случай имеет место тогда, когда .

Так как интенсивность спроса постоянна, то теку­щий объем запаса (рис. 3.5) изменяется в пределах одного периода по линейному закону

,

Функция затрат за период определяется выражением

(3.3)

Интеграл определяет произведение среднего объема запаса на время его существования [площадь фигуры, ограниченной осями координат и линией y ₀(t)]. Средние затраты в единицу времени

Так как возникновение дефицита не допускается, то объем за­паса в начале периода должен быть равен спросу за период, то есть y=lT. Учитывая, что находим

(3.4)

Приравнивая нулю производную этой функции по у, находим

(3.5)

Подставляя у* из формулы (3.5) в выражение (3.4), определим минимальные затраты на пополнение и хранение запасов в единицу времени:

(3.6)

Формулы (3.5) и (3.6) известны как формулы Уилсона, причем у* – это экономический размер заказа.

Если пополнение осуществляется мгновенно, то заказ подается в моменты времени t_з=T*, объем заказа S=y'*.

При задержке поставки на фиксированное время т заказ необходимо подавать в момент снижения объема запасов до величины

,

где tl – спрос за время поставки. В этом случае поставка будет поступать на склад в момент исчерпания запаса.

При случайной задержке поставки точку заказа определяют по правилу

,

где и – математическое ожидание и среднее квадратическое отклонение времени задержки поставки. Коэффициент k опреде­ляет резервный запас, который «демпфирует» случайные колебания времени задержки поставки. Значениям k= 1, 2, 3 соответствуют вероятности возникновения дефицита q =0,17; 0,025; 0,005 – для нормального; q= 0,13; 0,05; 0,018 – для экспоненциального и q= 0,211; 0,067; 0 – для равномерного закона распределения време­ни задержки поставки.

Если требуемое значение q не соответствует указанным значе­ниям, то коэффициент k рассчитывают следующим образом.

Очевидно, что дефицит отсутствует, если время задержки по­ставки в данном периоде не превышает величины , то есть

,

где – плотность распределения времени задержки поставки. Для экспоненциального распределения

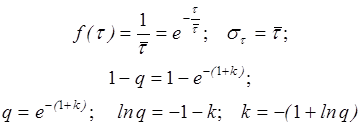
Аналогично точку заказа определяют, если имеют место слу­чайные колебания как времени задержки поставки, так и спро­са.

Следует подчеркнуть, что такой подход к определению парамет­ров стратегии управления запасами при случайной за­держке поставки и (или) вероятностном спросе яв­ляется приближенным. Для определения оптимальных параметров стратегии управления запасами необходимо исследовать вероятностную модель СУЗ.

3.2.2.Мгновенная поставка, возникновение дефицита
допускается.

График измене­ния текущего объема запа­са показан на рис. 3.6, где y ₁ – максимальный уровень запаса, Т ₁ – период пополнения.

Начальный запас в каждом пе­риоде будет исчерпан к моменту времени t ₁, то есть .

На интервале [0, t ] y ₀ (t) >0 и имеют место издержки хранения

На интервале [ t ₁, T ₁] y ₀ (t)< 0 (имеет место дефицит), и склад выплачивает штраф в размере

Знак «минус» перед интегралом учитывает, что дефицит равен объему запаса с противоположным знаком.

Функция затрат в единицу времени

(3.7)

Для определения оптимальных параметров стратегии управления запасами приравниваем производные функции (3.7) по у ₁ и T ₁нулю, то есть

 

Из первого уравнения находим

(3.8)

и, подставляя его во второе уравнение, получим

(5.9)

Подставляя выражение (3.9) в уравнение (3.8), находим

(3.10)

Из формулы (3.7) с учетом выражений (3.9) и (3.10) находим минимальные затраты в единицу времени на пополнение, хранение запасов и выплату штрафов:

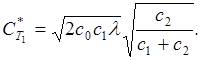(3.11)

Из выражений (3.9) – (3.11) и формул Уилсона (3.5) и (3.6) следует, что задалживание спроса (то есть ликвидация недостач пу­тем накопления требований до очередной поставки и выплаты штрафов) позволяет в раз уменьшить максимальный уровень запаса, минимальное значение функции затрат и частоту заказов (увеличить период пополнения) по сравнению со случаем отсутствия дефицита. Если c ₂>> c ₁, то и формулы (3.9) – (3.11) совпадают с формулами Уилсона.

Объем заказа при наличии дефицита

(3.12)

превышает объем заказа при отсутствии дефицита в раз.

При фиксированной задержке на время t заказ подается в мо­мент t ₃ снижения объема запаса до уровня

Учитывая выражения (5.10) и (5.12), находим

Если t = 0, то в момент подачи заказа на складе имеет место максимальный дефицит объемом .