Смешанные системы массового обслуживания

СМО с ограниченным временем ожидания характеризуется тем, что уменьшение числа заявок в ней происходит как в результате завершения обслуживания одной из заявок, так и в результате ухода заявок из очереди с интенсивностью v.

Если число заявок в системе k<n, то l_{k,k- 1}= km.. Если в очереди имеется r заявок (k=n+r), то переход из со­стояния S_k в состояние S_{k- 1} осуществляется или в результате за­вершения обслуживания одной из п заявок, или в результате ухода из очереди одной из r заявок, то есть

Таким образом, для СМО с ограниченным временем ожидания

(2.45)

Граф состояний системы изображен на рис. 2.6 (п= 2 ).

Подставляя выражения (2.45) в формулы (2.16) и 2.17), как и в случае СМО с конечной очередью, получим

(2.46)

(2.47)

. (2.48)

Определим основные показатели эффективности системы. Сред­няя длина очереди

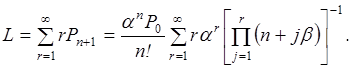(2.49)

На каждую из L заявок, находящихся в очереди, действует по­ток уходов интенсивности v, то есть в среднем в единицу времени из очереди уходит Lv заявок. Следовательно, абсолютная пропуск­ная способность

; (2.50)

относительная пропускная способность

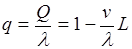(2.51)

вероятность отказа в обслуживании

; (2.52)

среднее число занятых приборов

; (2.53)

вероятность того, что любая заявка будет обслужена,

(2.54)

При вычислениях в формулах (2.46) и (2.49) в качестве при­ближенного значения для бесконечных сумм берется сумма конеч­ного числа l –1 членов, а остаток оценивается следующим об­разом:

.

Из выражений (2.50) – (2.54) следует, что основные показа­тели СМО можно вычислить через Р_отк, причём для определения Р_отк используют таблицы с тремя входами: n, a, b.

СМО с ограниченным временем пребывания характеризуется тем, что заявка может уйти необслуженной как из очереди, так и после начала обслуживания. Интенсивность перехода данной си­стемы из состояния S_k в S_{k- 1} (уменьшения числа заявок)

Подставляя выражения (2.9) и (2.55) в формулы (2.16) и (2.17), можно определить вероятности состояний данной системы.

Если одновременно накладывается ограничение на время ожи­дания (пребывания) и длину очереди, то число состояний системы конечно и равно п+т+ 1, а интенсивности переходов определяют­ся формулами (2.45) или (2.55), в которых r = 1, 2,..., т. Типич­ным примером системы данного типа является вычислительное устройство, которое может одновременно обрабатывать п сооб­щений и имеет буферную память для хранения т сообщений. По­ток сообщений – простейший поток интенсивности l, время обра­ботки одного сообщения , информация теряет свою ценность че­рез время . Граф состояний для случая n =2, m= 3 изображен на рис.
2.7.