СМО с отказами является частным случаем СМО с конечной очередью при m =0. Полагая в формулах (2.25) – (2.29) т= 0, найдем показатели эффективности СМО с отказами:
– вероятность простоя всех обслуживающих приборов из выражения (2.26)
; (2.34)
– вероятность того, что в системе находится k заявок, из формулы (2.27)
; (2.35)
– вероятность отказа в обслуживании из выражения (2.29)
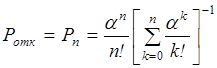; (2.36)
– абсолютная и относительная пропускная способность системы и среднее число занятых приборов
(2.37)
Зависимости (2.34) – (2.36) были впервые получены датским инженером А.К.Эрлангом и поэтому известны как формулы Эрланга.
Советский ученый Б.А.Севастьянов доказал, что формулы Эрланга справедливы при любом законе распределения времени обслуживания, но при конечном и постоянном значении его математического ожидания. Это позволяет использовать соотношения (2.34) – (2.37) для решения широкого класса практических задач.
