-Квадратная матрица называется
треугольной если все элементы
расположенные по одну сторону
диагонали равны нулю
-Матрица содержащая в себе один
столбец или строку называется
вектор столбцом вектор строкой
-Матрица полученная заменой строк
столбцами наз-ся транспонированной
-Минором некоторого элемента aij
определителя n-го порядка наз-ся
определитель (n–1)-го порядка,
полученный из исходного путём
вычёркивания строки и столбца,
на пересечении которых нах-ся
выбранный элемент.
- Алгебраическим дополнением
элемента aij определителя наз-ся
его минор, взятый со знаком «+»,
если сумма i+j чётное число,
и со знаком «-», если эта сумма неч.
- Правило треугольников


Свойства определителей
-Определитель матрицы не изменится
при транспонировании матрицы
-При перестановке двух IIрядов
определитель меняет знак на
противоположный
-Определитель имеющий два
одинаковых ряда равен нулю
-Общий множетель элементов
какоголибо ряда определителя
можно вынести за знак определителя
-Если элементы какого-либо ряда
определителя представляют собой
суммы двух слагаемых то опред.
может быть разложен на сумму
двух соответствующих определителей
-Определитель не изменится если
к элементам одного ряда прибавить
соответствующие элементы II ряда,
умноженные на любое число
-Величина определителя не меняется,
если по всем эл-ам ряда добавить соотв.
эл. др. ряда, умножен. на любое число к
-Величина опред. равна сумме пр-ий
эл. некоторого ряда на их алгебраич. доп.
Вычисл. опред. разложением по 1-ой стр.
det  =
=  = a11 a22 - a12 a21,
= a11 a22 - a12 a21,
 =
= 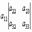 -
-  +
+ 






