Смысл. Св-ва дифференциала

limy=A, y=A+a

limDy/Dx=y`, Dy/Dx=y`+a, Dy=y`Dx+aDx

Dx®0

Dy=y`Dx+e, где e-б.м.в., величина более

высокого порядка малости,, чем Dx(a), и

ее можно отбросить.

dy=y`Dx

Дифференциалом ф-ции наз. величина,

пропорциональная б.м. приращению аргумента

Dх и отличающаяся от соответствующего

приращения ф-ции на б.м.в. более высокого

порядка малости, чем Dх.

Если y=x, то dy=dx=x`Dx=Dx, dx=Dx

Если y¹x, то dy=y`dx, y`=dy,dx

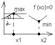
Геометрический смысл: дифференциал –

изменение ординаты касательной, проведенной

к графику ф-ции в точке (x₀,f(x₀)) при изменении

x₀ на величину Dx

Св-ва:
1. (U±V)`=U`±V`, то (U±V)`dx=U`dx±V`dx,

d(U±V)=d(U±V)

2. (UV)`=U`V+V`U, то (UV)`dx=V`dU+U`dV

3.d(c)=c`dx=0*dx=0

4. d(U/V)`=(V`dU-U`dV)/V².

Теорема Ролля.

Если функция f(x) непрерывна на

заданном промеж/ [a,b] деффер. на

интервале (a,b) f(a)=f(b) то существует т. с

из интерв. (a,b), такая, что f’(c)=0.