Несмотря на то что определение окружности учащимся не дается, необходимо познакомить их со свойством точек окружности.
Подготовительное упражнение.
Учитель отмечает на доске какую-нибудь точку и обозначает ее буквой О (учащиеся выполняют то же самое в своих тетрадях). Далее учитель отмечает сначала одну, затем другую, третью, четвертую точки, каждая из которых находится на расстоянии 2 см от точки О. При этом можно использовать линейку или циркуль.
В результате получится такой чертеж:
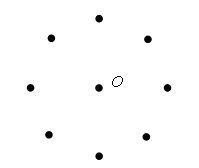
– Можно отметить еще очень много точек, каждая из которых находится на расстоянии 2 см от точки О. Давайте представим себе, что нам удалось отметить все такие точки. Все точки, находящиеся на расстоянии 2 см от точки О, образуют фигуру, которую называют словом «окружность». Чтобы изобразить окружность, не нужно отмечать все точки, для этого нам понадобится циркуль. Посмотрите, как нужно правильно им пользоваться.
Отмечаем точку О; она будет центром окружности. Берем циркуль и немного разводим в стороны концы его ножек (не обязательно на 2 см, можно взять любое расстояние). Держа циркуль правой рукой (покажите), ставим в точку О ножку циркуля с иглой. Чуть отклоняя циркуль, поворачиваем ножку с карандашом вокруг точки О, касаясь карандашом доски. Получается окружность.
Теперь вы сами попробуйте начертить окружность в тетрадях. Отмечайте центр окружности. Далее берите циркуль. Проводя окружность, придерживайте тетрадь левой рукой. Окружность чертить трудно, поэтому придется потренироваться. Изобразите несколько окружностей.
– Рассмотрите чертеж на доске.
– На какие две группы можно разделить фигуры на рисунке?
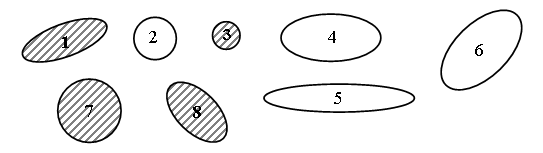
– Запишите номера и общее название фигур каждой группы.
I группа – это линии (2, 4, 5, 6);
II группа – это фигуры (1, 3, 7, 8).
– Разделите эти же фигуры на 2 группы по другому признаку. Запишите номера фигур новых групп и объясните, в чем сходство фигур каждой группы.
I группа – это линии, которые являются границей круга, т. е. окружности (2).
II группа – это линии, которые являются границей овала (4, 5, 6).
III группа – фигуры, которые являются кругами (3, 7).
IV группа – фигуры, которые являются овалами (1, 8).
– Рассмотрите рисунок. Что здесь изображено? (Рис. а – круг, рис. б – окружность.)
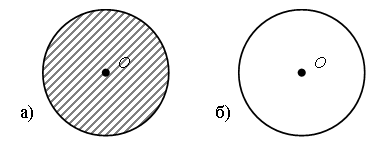
– Каким инструментом удобно чертить окружность?
– Как называется точка О? (Центр окружности.)
– Отметьте любую точку на окружности. Соедините отрезком центр окружности с этой точкой. Этот отрезок называют радиусом.
| Если соединить любую точку окружности с ее центром, то получится отрезок, который называется радиусом окружности. |
– Постройте еще несколько радиусов этой окружности.
– Назовите радиусы на чертеже. (ОА, ОВ, ОС, OD, ОЕ.)
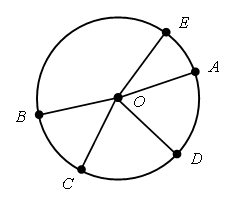
– Сколько радиусов можно провести в одной и той же окружности?
– Измерьте длину каждого радиуса. Почему все радиусы окружности имеют одну и ту же длину?
Задание № 1 (с. 72).
– Какие предметы похожи на окружность? (Обруч, колесо, солнце и т. д.)
– Рассмотрите чертеж (с. 72 учебника).
– Покажите концом указки окружность (конец указки должен скользить по окружности).
– Покажите центр окружности. (Это точка.)
– Покажите радиус окружности. (Это отрезок.)
– Рассмотрите правую часть чертежа. Что здесь изображено? (Способ построения окружности с длиной радиуса 4 см.)
– Расскажите о порядке работы.
– Выполните данное построение окружности на доске и в тетрадях.
Задание № 2 (с. 72).
Используя циркуль, учащиеся строят в тетради три разные окружности.
– Отметьте центр каждой окружности.
– Укажите длину радиуса.

Задание № 3 (с. 72).
Перед выполнением задания необходимо обсудить с учащимися план построения окружности.
1. Отметить произвольную точку О – центр окружности.
2. Установить расстояние между ножками циркуля, равное 5 см, то есть длине радиуса окружности.
3. Выполнить построение окружности.
Задание № 4 (с. 72).
Учащиеся строят окружность и проводят в ней три радиуса.
– Сколько еще радиусов можно провести для этой окружности?




