II. Устный счет.
1. Рассмотрите фигуры. Определите, чем каждая следующая отличается от предыдущей. Нарисуйте четвертую фигуру, не нарушая закономерности.
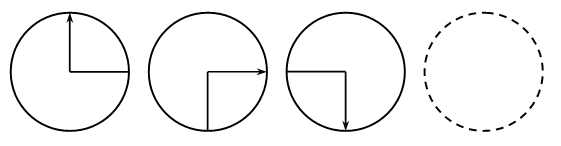
2. Решите задачу.
На велогонках стартовали 70 спортсменов. На первом этапе с трассы сошли 4 велосипедиста, на втором – 6.
– Сколько спортсменов пришло к финишу?
– Выберите выражение, которое является решением задачи:
| 6 + 4 | 6 – 4 | 70 – 6 |
| 70 – 6 – 4 | 70 – 4 – 6 | 70 – 4 |
3. Вставьте знаки арифметических действий, чтобы получились верные равенства:
| 8 … 7 …6 = 9 | 6 … 6 … 4 = 8 |
| 15 … 7 … 1 = 9 | 7 … 7 … 6 = 8 |
| 4 … 8 … 3 = 9 | 9 … 3 … 4 = 8 |
4. Анализ чертежа.
– На какие две группы можно разделить фигуры на рисунке?

– Запишите номера и общее название фигур каждой группы.
– Сравните свои группы с такими:
I группа – фигуры 1, 3, 8;
II группа – фигуры 2, 4, 5, 6, 7.
– Они похожи? По какому признаку выделены эти группы?
III. Сообщение темы урока.
– Рассмотрите данный на доске чертеж:

– Чем похожи и чем отличаются рисунки слева и справа?
– Сегодня на уроке мы узнаем, чем отличается окружность от круга.
IV. Изучение нового материала.
Задание № 6 (с. 78).
– Рассмотрите рисунок в учебнике.
– Назовите, что имеет в очках форму окружности, а что – круга. (Стекло – это круг, а оправа – окружность.)
| Окружность представляет границу круга, а круг – это окружность вместе с внутренней областью, ограниченной этой окружностью. |
– В этом и состоит различие между кругом и окружностью.
– Начертите в тетради какой-нибудь круг. В отличие от окружности круг нужно закрасить.
– Отметьте центр этого круга и радиус.
Задание № 7 (с. 73).
Две разные окружности могут иметь один и тот же радиус лишь в том случае, если их центры – различные точки. (После устного обсуждения задания попросите учащихся в тетрадях построить две разные окружности с одним и тем же радиусом.)
Задание № 8 (с. 73).
Задание направлено на развитие внимания учащихся.
На первом чертеже изображено 6 окружностей, на втором чертеже – 10 окружностей.
Задание № 5 (с. 73).
Чертеж:

V. Повторение пройденного материала.
1. Работа в печатной тетради № 1.
Задание № 106.
Среди данных фигур только фигура № 3 является окружностью. По ходу выполнения задания обратите внимание учащихся на фигуру № 1 (круг). Попросите детей сравнить круг и окружность. Выясните, чем они похожи и чем отличаются.
Задание № 107.
Учащиеся объясняют, что при построении радиуса надо сначала выбрать произвольную точку на окружности. Соединив центр окружности и выбранную точку отрезком, мы получим радиус.
Затем можно переходить к измерению длины радиуса (длины построенного отрезка). Она равна 2 см.
Задание № 108.
Так как в условии не указана длина радиуса, то ее мы можем выбрать произвольно. Значит, окружностей с центром в точке Р можно построить сколько угодно.
Чертеж:

– Сколько окружностей у вас получилось?
Задание № 110.
Если у слабоуспевающих учащихся возникнут трудности при построении окружности, предложите им воспользоваться карточкой-помощницей.

Учитель должен обратить внимание учащихся на то, что для измерения длины радиуса построенной окружности необязательно его строить. Достаточно измерить расстояние между точками В и С. Исходя из условия задания, можно построить единственную окружность, так как задан не только центр (В), но и радиус (ВС).
2. Работа по учебнику.
Задание № 15 (с. 75).
– Прочитайте текст. Является ли он задачей?
– Что известно в задаче?
– Что требуется узнать?
При решении этой задачи учащиеся могут рассуждать следующим образом: «На каждой полке 15 книг, следовательно, на двух полках вместе: 15 + 15 = 30 (книг). Всего с двух полок сняли столько книг, сколько было на первой полке, то есть 15 книг, следовательно, на полках осталось: 30 – 15 = 15 (книг)».
VI. Итог урока.
– Что нового узнали на уроке?
– Чем отличаются окружность и круг?




