1. Работа по учебнику.
Задание № 7 (с. 78).
Учащиеся записывают условие, используя «окошки».
| 6 + = 16 | – 14 = 5 | 14 – = 5 |
| 16 – 6 = 10 | 14 + 5 = 19 | 14 – 5 = 9 |
| 6 + 10 = 16 | 19 – 14 = 5 | 14 – 9 = 5 |
– Какие знания помогли вам выполнить это задание?
Задание № 10 (с. 78).
– Прочитайте задачу.
– Что известно в задаче? Что требуется узнать?
– Запишите кратко условие задачи и решите ее.

Решение: 5 + 5 + 5 + 5 + 10 + 10 = 40 (коп.)
Ответ: 40 копеек.
Задание № 11 (с. 78).
– Прочитайте текст. Является ли он задачей? Почему?
– Что известно в задаче? Что требуется узнать?
– Запишите кратко условие задачи в таблице.

Решение:
1) 15 + 15 = 30 (р.) – стоят 2 бутылки молока.
2) 30 + 36 = 66 (р.) – стоимость всей покупки.
Ответ: 66 рублей.
2. Работа в печатной тетради № 1.
Задание № 114.
Вспомните с учащимися, что луч (в отличие от отрезка) – бесконечная фигура, поэтому, для того чтобы ответить на вопрос задания в отношении каждого из лучей, надо сначала правильно показать этот луч на чертеже.
Выполняя задание, дети должны прийти к выводу, что окружность пересекают лучи CD, FN иотрезок КМ.
Справочный материал для учителя
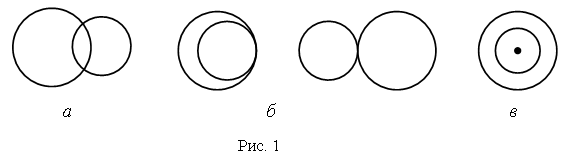
Учащимся предлагаются задания, в которых представлены разнообразные случаи расположения многоугольников, окружностей, отрезков, лучей; при этом фигуры могут пересекаться либо не пересекаться. Интересны примеры взаимного расположения двух окружностей:
а) окружности пересекаются в двух точках;
б) касаются одна другой (два случая – внутреннее и внешнее касание);
в) расположены концентрически (имеют общий центр).
Прямая, проходящая через точку окружности перпендикулярно к радиусу, проведенному в эту точку, называется касательной. При этом данная точка окружности называется точкой касания. На рисунке 2прямая а проведена через точку окружности А перпендикулярно к радиусу ОА. Прямая а является касательной к окружности. Точка А является точкой касания. Можно сказать также, что окружность касается прямой а в точке А.

Говорят, что две окружности, имеющие общую точку, касаются в этой точке, если они имеют в этой точке общую касательную (рис. 3). Касание окружностей называется внутренним, если центры окружностей лежат по одну сторону от их общей касательной (рис. 3, а). Касание окружностей называется внешним, если центры окружностей лежат по разные стороны от их общей касательной (рис. 3, б).

VI. Итог урока.
– Что нового узнали на уроке?
– Назовите признаки окружности.
Домашнее задание: № 8, 9 (учебник).
Урок 40
Взаимное расположение фигур на плоскости
Цели урока: рассмотреть случаи взаимного расположения двух окружностей; совершенствовать навыки решения практических задач; продолжить подготовительную работу по введению умножения и деления; развивать внимание и логическое мышление.
Ход урока






