Теория связи и теория информации

Итак, кибернетика — наука, изучающая процессы связи, управления и регулирования в различных систе­мах. Что же такое система?

Система — организованный комплекс элементов,

связанных друг с другом и выполняющих определенные
функции, в соответствии с программой всей  системы.

Программа, по Н. М. Амосову, это последователь­ность изменений системы в пространстве и во времени, заложенная в структуре самой системы. Если рассмат­риваются подсистемы, то программы для них могут по­ступать извне, а не быть заложенными в собственной структуре.

Под связью понимается взаимодействие элементов друг с другом, в процессе которого они обмениваются веществом, энергией и информацией Сущность кибер­нетики состоит в исследовании процессов управления. А содержанием процессов управления является прием, хранение, переработка и передача информации. Поэто­му в дальнейшем под связью мы будем понимать лишь передачу информации от одного элемента системы к другому.

Теоретическую основу систем связи составляют об­щая теория связи и количественная теория информа-

12

 

ции. Для их понимания необходимо знание теории ве­роятностей.

Предмет теории вероятностей составляют массовые случайные события, которые обладают устойчивой ча­стотой появления. Под случайным событием в теории вероятностей подразумевается такое событие, которое может произойти или не произойти в данных условиях. Согласно материалистической диалектике, случайность является формой проявления необходимости. Теория вероятностей позволяет точно описывать случайные яв­ления, и в этом состоит ее огромная ценность.

Допустим, мы имеем нервно-мышечный препарат и производим раздражение нерва током пороговой силы. Пусть мы произвели 100 опытов по раздражению нер­ва. При этом оказалось, что в 95 случаях мышца от­ветила сокращением на раздражение, а в 5 случаях — не ответила. Отношение числа событий, в которых на­ступило сокращение, к общему числу опытов будет на­зываться частотой появления сокращения мышцы. В данном случае это 95/100 = 0,95. Если в общем случае обозначим общее число испытаний N, а число испыта­ний, в которых наступило данное событие (назовем его Л), — п и частоту появления события А обозначим Ф (A), то

(1)

                                                                                         

Допустим, мы провели еще несколько серий испыта­ний, каждая из которых содержит по 100 опытов, и по­лучили следующие частоты появления сокращения мышцы: 97, 93, 94, 96. Если мы теперь сложим частоты всех пяти серий и разделим полученную сумму на ко­личество серий, то получим вероятность сокращения мышцы:

 

 

Таким образом, вероятность — это среднее значение частоты появления события при массовых испытаниях.

Если в сериях одинаковое количество опытов N, то можно найти среднее количество опытов в серии п, в которых наступает событие А. Тогда отношение сред­него количества данных событий А к общему количест-

13

 

ву событий в серии и будет вероятностью Р(А) появле­ния события А:

(2)

Вероятность вычисляется тем точнее, чем более массовым является испытание.

Из уравнения (2) следует, что вероятность может принимать значения от 1 до 0: 1≥Р(А)≥0. События, вероятность которых равна нулю, называются невозможными, а вероятность которых равна единице, — достоверными ¹Вероятность всегда показывает долю дан­ных событии в общем количестве событий и поэтому является объективной мерой возможности данного со­бытия. Например, если известно, что Р(А) = 0,3, а Р (В)=0,6, то это говорит о том, что событие А насту­пает в среднем в 3 случаях из 10 и в 2 раза реже, чем событие В.

Сложение вероятностей. Говоря о событиях, мы раз­личаем события совместимые и несовместимые. Не­сколько событий называются несовместимыми в дан­ном опыте, если никакие два из них не могут появиться вместе, т. е. если события взаимно исключаются. В рас­смотренном примере имелись как раз несовместимые события: или есть сокращение мышцы, или нет его. Ес­ли же при осуществлении одного события возможны и другие события, то они называются совместимыми.

 

 

Пусть при проведении некоторой массовой операции было уста­новлено, что в каждой серии из N единичных операций наблюдается

всреднем:

причем в каждой операции наблюдается только одно из этих событий. Тогда вероятности событий равны соответственно:

 

и т. д. Какова вероятность того, что в некоторой еди­ничной операции может наступить какое-либо одно из этих событий, безразлично какое?

¹ В (вариационной статистике событие считается достоверным, если его вероятность больше, а вероятность противоположного собы­тия '(ошибки) меньше определенных величин. Ори обработке цифро­вого материала в биологии и медицине результат обычаю считается достоверным, если вероятность ошибки меньше 0,05.

14

Интересующее нас событие можно назвать А₁ либо А₂, либо... и записать А₁+А₂+А₃+... Это событие в се­рии из N операций наступает в среднем n₁ +п ₂ +п ₃ +... раз. Искомая вероятность, что наступит одно из этих событий, равна:

 

 

Вероятность наступления в некоторой операции ка­кого-либо одного (безразлично какого именно) из со­бытий А ₁ ,А ₂ ,А ₃... равна сумме вероятностей этих со­бытий, если они несовместимы между собой.

Пример. В некоторой популяции животных име­ются самцы, самки и детеныши. Вероятность того, что первое выбранное животное будет самцом Р₁ = 0,2, сам­кой— Р ₂ =0,7, детенышем — Р ₃ = 0,1. Найти вероятность того, что первое выбранное животное будет или сам­цом, или самкой.

Данные события являются несовместимыми: живот­ное не может быть сразу и самцом и самкой. Интересу­ющую нас вероятность находим из уравнения (3):

Правило сложения вероятностей справедливо лишь для несовместимых событий, в противном случае оно становится невероятным и приводит к грубым ошибкам.

Вероятности противоположных событий. Пусть в се­рии из N событий событие Л наступает в среднем п раз. Тогда среднее количество ненаступления событий Л равно N — п. Данное событие, т. е. ненаступление со­бытия Л, мы будем называть противоположным собы­тием и обозначать Л. Таким образом, противоположны­ми являются два таких события, что в одном опыте на­ступает только какое-либо одно из этих событий. Оп­ределим, чему равна сумма вероятностей противопо­ложных событий:

 

Сумма вероятностей противоположных событий равна

единице. В нашем примере с нервно-мышечным препаратом вероятность сокращения мышцы составляла 0,95;

                                                         15

следовательно, вероятность отсутствия сокращения рав­на 1—0,95=0,05.

Сумма вероятностей всех событий серии. Пусть в серии из N событий всего т различных событий: А₁, А₂, А₃...А_m. В каждом единичном опыте должно наступать любое только из этих событий. Определим, чему равна сумма вероятностей всех событий серии.

 

Данное положение называется теоремой о полной си­стеме событий: сумма вероятностей всех событий серии равна единице.

На этой теореме основывается априорный (до опытный) расчет вероятностей. Если, например, известно, что одно событие имеет вероятность 0,3, а несовмести­мое с ним событие — 0,4, то в данной системе событий имеются еще какие-то события и их вероятность равна 1—0,3—0,4 = 0,3. Наш пример с популяцией животных содержит полную систему событий, где сумма вероят­ностей всех событий равна единице.

Вероятность наступления совместимых событий. Ес­ли имеется несколько совместимых событий и они яв­ляются независимыми (когда наступление одного собы­тия не зависит от наступления других), то вероятность совместного наступления Р(А₁*А₂*А₃*...А_п) любого чис­ла взаимно независимых событий равна произведению вероятностей этих событий:

В заключение приведем пример, в котором исполь­зуем большинство установленных правил. Известно, что для группы населения частота встречаемости или веро­ятность обнаружения зачатков сколиоза у детей школь­ного возраста Р(с)=0,7, а вероятность начинающейся порчи зубов (кариеса) Р(к)=0,6. Определить следую-                   16

щие вероятности: Р(ск)—вероятность наличия сразу обоих расстройств, Р(с')—вероятность наличия только сколиоза, Р(к') —вероятность наличия только кариеса,

Рск)—вероятность отсутствия обоих расстройств.

Наличие сколиоза и наличие кариеса являются независимыми событиями, поэтому вероятность их одно­временного наличия у одного ребенка будет равна про­изведению вероятностей этих событий:

Р (ск) = Р (с) * Р (к) = 0,7*0,6 = 0,42.

Если из вероятности Р(с) наличия сколиоза вычесть вероятность наличия сразу обоих расстройств Р(ск), то и соответствии с правилом сложения вероятностей (3) получим вероятность наличия только сколиоза:

Р (с') = Р(с) — Р(ск) =0,7 — 0,42 = 0,28.

Таким же образом:

Р(к') =Р(к) — Р(ск) =0,6 —0,42=0,18.

Если воспользуемся правилом о сумме вероятностей противоположных событий, то получим вероятность от­сутствия сколиоза:

Р(с) = 1—Р(с) = 1 — 0,7=0,3.

Таким же образом:

Р(к) = 1 — Р(к) = 1 —0,6 = 0,4.

Вероятность отсутствия обоих расстройств будет равна произведению вероятностей отсутствия сколиоза и от­сутствия кариеса:

Р (ск) = Р (с) Р (к) = 0,3*0,4 = 0,12.

Мы вычислили все интересующие нас вероятности и по­лучили полную систему событий. Сумма вероятностей всех возможных событий равна единице:

Р (ск) + Р (с') + Р (к') + Р (ск) = 0,42 + 0,28 + 0,18 + 0,12 = 1.

На этом мы заканчиваем рассмотрение вопросов тео­рии вероятностей. Этим вопросам было уделено срав­нительно большое внимание в связи с тем, что в буду­щем вероятностные методы получат широкое распро­странение в медицине.

Система связи. В любой кибернетической системе имеются управляющая часть и объект управления, со-

        

 

2 Медицинская биофизика                                                                          17

 

единенные каналами связи. Связь состоит в восприя­тии, хранении и передаче информации. Устройство, ре­ализующее связь, называется системой связи. Система связи, по Шеннону, состоит из пяти частей (схема 1).

Источник сообщений подает сообщения, которые в передатчике превращаются в сигналы. Сигналы пере-

Схема 1. Схема обобщенной системы связи ((по Шеннону, 1948).

даются по каналу связи к приемнику, который снова превращает их в сообщения и направляет полу­чателю.

В качестве примера может быть приведена такая си­стема: книга — глаза — нервы — подкорковые зритель­ные центры — кора больших полушарий.

Под сообщением подразумевается все то, что подле­жит передаче в системе связи, поступает навход пере датчика или создается на выходе приемника. Сообще­ния бывают двух видов: непрерывные и дискретные Непрерывные сообщения имеют характер непрерывно изменяющейся величины, например изменяющейся величины кровяного давления, температуры, напряжения мышц, музыкальной мелодии. Дискретные сообщения состоят из отдельных, отличающихся друг от друга ступеней или градаций. Это, например, химические ча­стицы, действующие на хеморецепторы, азотистые ос­нования молекулы ДНК, точки и тире в азбуке Морзе.

В технике существуют специальные методы преобразования непрерывных сообщений в дискретные.

Для того чтобы сообщение было передано данной системой связи, оно должно быть преобразовано на входе этой системы в физическую форму, пригодную для передачи по ее внутренним каналам. Так, сообще­ние, имеющееся в читаемой книге, преобразовывается зрительными рецепторами в последовательность нерв­ных импульсов, пригодных для анализа нервной систе-

18

 

мой. Эта возникающая в системе связи в результате преобразования новая физическая форма сообщения называется сигналом. Сигнал является материальным носителем сообщения.

Канал связи - это та среда, в которой осуществ­ляется передача сигналов. В нервной системе сигнала ми являются нервные импульсы, а каналом связи—нерв­ное волокно. При гуморальном воздействии сигналом является химическое вещество (гормон, медиатор и пр.), а каналом связи — кровь и тканевая жидкость.

Обычно сигналы обладают сравнительно небольшой энергией. Для приемника сообщений неважно, какой энергией обладают сигналы. Для него важен сам факт появления сигнала, т. е. та информация, которую пере­носят данные сигналы. Каким же образом сигналы, пе­реносящие информацию, осуществляют управление про­цессами, если они обладают небольшой энергией? Дело в том, что информация является моделью того или иного процесса и сигналы, переносящие данную ин­формацию, только модулируют данный высокоэнергети­ческий процесс. По мнению У. Эшби, сигналы регулируют  потокэнергии в управляемой системе, хотя сам управляемый процесс развивается за счет собственной энергии. Так, мышечное сокращение вызывается и уп­равляется нервными импульсами, поступающими по нервному волокну, а сам процесс мышечного сокраще­ния осуществляется за счет энергии гидролиза АТФ. В данном случае сигналы — нервные импульсы — регу­лируют через ряд стадий (возбуждение цитоплазматических мембран, освобождение ионов кальция) расщеп­ление АТФ актомиозином и, следовательно, мышечное сокращение. Это положение можно проиллюстрировать и на примере работы анализаторов. Внешние раздра­жители (свет, звук и др.), которые играют роль сигна­лов, модулируют нервные процессы в анализаторах. По­следние развиваются за счет собственной энергии кон­центрационных градиентов.

Преобразование сообщения в сигналы, а также преобразование одних сигналов в другие, наиболее приемлемые дляпередачи по данному каналу, называется, кодированием.Кодирование происходит в передатчике сообщений. В приемнике сигналов происходит обратный процессе — декодирование, т. е. превращение сигналов снова в сообщения, которые воспринимает получатель.

2*                                                                                                                     19

 

Кодирование осуществляется с помощью элементов ко да: символов и позиций. Символы являются безраз­мерными величинами, которые качественно обозначают что-либо. Примерами символов могут служить буквы алфавита, математические знаки, нервные импульсы, молекулы пахучих веществ, азотистые основания в мо­лекуле ДНК и т. п.

Позиция является вторымэлементарным структурным звеном кодирования Позиции определяют пространственное и временное размещение символов при кодировании. При кодировании и декодировании сооб­щении и сигналов каждой позиции по определенным правилам ставится один из символов применяемого ко­да в соответствии с размещением символов по позици­ям исходного сообщения пли сигнала. Например, бук­венный текст при кодировании азбукой Морзе заменя­ется определенной последовательностью точек и тире. Каждая система кодирования имеет свои правила. На­пример, принцип кодирования интенсивности раздра­жителя в большинстве анализаторов заключается в том, что при увеличении интенсивности раздражите­ля происходит завышение частоты нервных импуль­сов в афферентных волокнах по логарифмическому закону.

В результате кодирования между исходным сооб­щением и возникающими при кодировании сигналами устанавливается однозначное соответствие. Это свойство сигналов быть однозначными с сообщениями, быть по­добными сообщению, называется изоморфностью. Изо­морфные сообщения и сигналы всегда содержат одну и ту же информацию, хотя она выражена разными сред­ствами. Например, буквенный текст и тот же текст, за­писанный азбукой Морзе, являются (изоморфными со­общениями. На основе изоморфности возможно точное (адекватное) отражение сообщения в сигналах.

Вычисление информации. Живая природа создала
множество различных типов систем связи. Одни из этих
систем более совершенны, другие — менее. Более эффективной будет такая система связи, которая' за единицу времени способна передать большее количество
сообщений. Как же оценивать сообщения? Для оценки
сообщений введено специальное понятие — информация, которая является количественной мерой сообщения.    

20

 

Сообщения и сигналы, которыми оперирует каждая система связи, относятся к категории случайных явлений. В любой момент времен» неизвестно, какое имен­но сообщение поступит на вход системы связи; сообще­ния, известные получателю, в передаче не нуждаются. События, о которых сообщается, нельзя предвидеть за­ранее, так как нет уверенности, что они произойдут, мим ожидаемым событием присуща неопределенность, которая затем устраняется по мере поступления информации. Согласно Шеннону, информация — это мера количества неопределенности, которая устраняется после получения сообщения. Мерой неопределенности событий является энтропия, подобно тому как она яв­ляется мерой неупорядоченности, хаотичности системы в термодинамике. Тогда информация, содержащаяся в сообщении, будет численно равна энтропии, исчезаю щей после получения сообщения.

Допустим, ожидается наступление какого-либо од­ного из N равновероятных событий. Относительно на­ступления этого события имеется неопределенность: мо­жет произойти с одинаковой вероятностью любое из этих событий. Количество неопределенности — энтропия Н —в данном случае равна двоичному логарифму от числа ожидаемыхсобытий:

  (7)

Если теперь получено сообщение о том, что произошло какое-то из этих событий, то неопределенность полно­стью устраняется и полученное сообщение будет содер­жать информацию, численно равную устраненной энт­ропии.

Информация, вычисленная по уравнению (7), выражается в битах –  двоичныхединицах. Определим, что такое один бит. Для этого правую часть уравнения (7) приравняем к единице:

отсюда N=2. Таким образом, информация 1 бит содер­жится в сообщении о том, что наступило одно из двух равновероятных событий. Это количество информации, необходимое для выбора одной из двух равновероят­ных возможностей, дает ответ по типу «да», «нет». На­пример, было известно, что должен родиться или маль­чик, или девочка. Тогда сообщение «родился мальчик» содержит 1 бит информации.

21

 

 

Пример. Сколько информации содержится в со­общении о том, что данный нуклеотид в молекуле ДНК содержит цитозин, если известно, что азотистых осно­ваний в молекуле ДНК содержится примерно поровну? Так как всего имеется 4 азотистых основания и коли­чество их одинаково, то данный нуклеотид может с оди­наковой вероятностью содержать любое из этих 4 ос­нований. В данном случае ожидается наступление одно­го из 4 равновероятных событий. Информация, содер­жащаяся в приведенном выше сообщении, будет равна 2 бит:

Н = log ₂ 4 = 2 бит.

Кроме единицы измерения информации бит, иногда применяется единица хартли. Эта единица получается, если при вычислении информации пользоваться не дво­ичным логарифмом, а десятичным:

1 хартли — количество информации, необходимое для выбора одной из десяти равновероятных возможностей. Соотношение для бит и хартли будет следующее:

1 хартли = log ₂ 10 = 3,3 бит, 1 бит = lg 2 = 0,301 хартли.

Выше было рассмотрено вычисление энтропии и ин-формации для самого простого случая, когда ожидае­мые события являются равновероятными. В том случае, если "ожидаемые" события неравно вероятны, вычисление энтропии и информации производится с помощью урав­нения Шеннона:

Н = -Σ P_i • log₂P_i                           (8)

i =1

где Σ — знак суммирования подзнакового выражения от 1 до п; P_i — вероятности всех ожидаемых событий от 1 до п; знак минус стоит потому, что логарифмы чи­сел от 0 до 1 отрицательны.

Пример. В некоторой популяции 20% всех жи­вотных являются самцами, 70%—самками, 10%—де­тенышами. Сколько информации содержится в сообще­нии, что данное животное является самцом? Опреде­лим вероятности всех ожидаемых событий. По опреде­лению вероятности (2) находим: вероятность того, что

22

 

случайно выбранное животное является самцом Р ₁= = 0,2, самкой — Р₂ = 0,7, детенышем — Р₃ = 0,1. Под­ставляя полученные вероятности в уравнение (8), на­ходим энтропию, которая была до получения сообще­ния:

Н = — [0,2 • log₂ 0,2 + 0,7 • log₂ 0,7 + 0, 1 • log₂ 0,1] = = — [—0,093—0,259—0,033] ==0,384 бит.

После получения сообщения о том, что животное — са­мец, энтропия стала равной нулю: Р₁=1, Р ₂=0, Р _з=0

и Н = — 1 * log ₂ 1 = 0 бит, поэтому приведенное сообщение содержит 0,384 бит информации.

Если после получения сообщения неопределенность полностью не устраняется, то для определения количе­ства информации необходимо взять разность между эн­тропией до получения сообщения и энтропией после по­лучения сообщения.

Некоторыми авторами для определения информации

в сообщениях предложено уравнение:

                                              

(9)

 

где Р₀ — вероятность наступления события до получе­ния сообщения; Р — вероятность наступления события после получения сообщения.

Уравнение (9) применимо для вычисления инфор­мации независимо от того, полностью или не полностью устраняется неопределенность после получения сообще­ния.

Пример. В русском алфавите 32 буквы, из них 8 — гласных. Сколько информации содержит сообще­ние, что данная буква гласная? До получения сообще­ния вероятность того, что данная буква гласная Р₀ = = 8/32 = ¹/₄ (по определению вероятности), после полу­чения сообщения Р=1 (событие достоверное). Инфор­мация, содержащаяся в приведенном сообщении Н = log ₂ Р/Р_о = log ₂ 1/¹/₄=2 бит.

Если передатчик выдает п сообщений в секунду и каждое сообщение содержит Н бит информации, то скорость передачи информации I передатчиком будет равняться:

I = пН.                                             (10)

Для нормальной работы системы связи необходимо, чтобы скорость передачи информации передатчиком

23

 

 

                                       

 

была не больше пропускной способности канала связи, приемника и воспринимающей способности получателя. Например, рецепторный аппарат должен посылать ин­формацию со скоростью не большей пропускной способ­ности афферентных нервных путей. Если же условие согласования скорости передачи информации по всем элементам системы связи не соблюдается, то часть ин­формации при передаче будет теряться. Максимальная скорость передачи информации в системе связи будет определяться элементом с наименьшей пропускной спо­собностью.

При передаче информации от передатчика к прием­нику по каналу связи часть информации теряется так­же вследствие помех, поэтому на схеме системы связи вместе с каналом связи изображен источник помех (схема 1). Борьба с вредным влиянием помех осущест­вляется путем многократного повторения сигнала. Это повторение может осуществляться двумя способами: повторением во времени и повторением в пространстве. В первом случае сигнал несколько раз подряд переда­ется по одному каналу связи. Повторение в пространст­ве осуществляется путем передачи одного сигнала по нескольким параллельным каналам. Например, одни нейрон соединяется с другим несколькими синаптическими окончаниями и посылает импульсы сразу по всем параллельным отросткам.

Кодирование наследственной информации. Как из­вестно, наследственная информация закодирована б структуре ДНК. Последовательность расположения азо­тистых оснований в молекуле ДНК определяет после­довательность расположения аминокислотных остатков в молекуле белка. Подсчитаем, какое количество ин­формации содержится в ДНК человека. ДИК содержит всего 4 азотистых основания: аденин, гуанин, цитозин и тимин. Любой произвольно выбранный нуклеотид может содержать одно из этих оснований, т. е. следует ожидать наступления одного из 4 событий. Тогда ин­формация, приходящаяся на одну позицию в молеку­ле ДНК — па один нуклеотид, будет Н = log₂4=2 бит. М. Перутцем было определено, что в ДНК всех хромо­сом сперматозоида человека содержится 10⁹ нуклеотидов. Тогда общее количество информации, содержащей­ся в ДНК человека, будет равно 2-Ю⁹ бит. Это огром­ное количество информации — 2 млрд. ответов по типу

24

 

«да», «нет». Данная цифра несколько завышена. Мы приняли, что вероятности наличия азотистых оснований в данном нуклеотиде одинаковы. На самом деле эти ве­роятности различны, поскольку азотистые основания содержатся в молекуле ДНК не в одинаковом количе­стве.

Подсчитаем количество информации, необходимое для синтеза одной молекулы белка. Всего имеется 20 различных аминокислот. Тогда на одну позицию в мо­лекуле белка — на одну аминокислоту — будет прихо­диться Н=log₂20л;4 бит. Молекула белка содержит в среднем 10³ аминокислотных остатков. Тогда в среднем молекула белка содержит 4-Ю³ бит информации. Если разделить количество информации, содержащейся в ДНК, на количество информации, содержащейся в мо­лекуле белка, то будет получено количество молекул белка, способных синтезироваться в соответствии с ин­формацией, полученной от ДНК: 2 -10⁹/4 -10³=500 000. Таким образом, ДНК человека содержит такое количе­ство информации, которого достаточно для синтеза 500 000 различных белков. Считается, что один белок — это один фермент, а один фермент кодируется одним геном. Ген — дискретная единица наследственной ин­формации, определяющая один признак организма. Тогда можно отметить, что ДНК человека содержит 500 000 генов, т. е. хранит информацию о 500 000 при­знаках данного организма. За счет этой информации че­ловек проходит весь путь эмбрионального развития жи­вых организмов, начиная от простейших.

ТЕОРИЯ РЕГУЛИРОВАНИЯ

Кибернетическая система имеет в своем составе уп­равляемую и управляющую части, соединенные канала-Ми связи. Саморегулирующиеся системы содержат, как правило, прямую и обратную связи между управляющей и управляемой частями системы (рис. 1).

Устройство управления, которое является элементом Управляющей части системы, производит управление соответствующим объектом. Существует множество оп­ределений управления. По А. И. Бергу, управление — это процесс перевода системы из одного состояния в другое путем воздействия на ее переменные.

25

 

 

 

Любой объект управления характеризуется какой-либо регулируемой величиной. Например, кровь и сер­дечно-сосудистая система как объекты управления име­ют следующие регулируемые величины: кровяное дав­ление, осмотическое давление, концентрацию глюкозы, кислорода В крови И пр. Объект управления является динамической системой: его регулируемая, величина всегда имеет тенденцию к изменению в результате дей­ствия различных возмущений. Возмущением считается, любое внешнее воздействие наобъект управления, при водящее к изменению регулируемой величины. Напримёр, для такой регулируемой величины, как концентрация глюкозы в крови возмущениями являются поступ­ление глюкозы из печени или кишечника в кровь и на оборот—поступление глюкозы из крови в ткани.

В результате передачи сигнала по каналу прямой связи к объекту. Ранее отмечалось, что сигналы управления модулируют энергетические процессы в объекте управ­ления, в результате чего состояние объекта управления изменяется в соответствии с принятыми сигналами, т. е. в соответствии с принятой информацией. При этом ре­гулируемая величина принимает какое-то значение.

В простых системах управление осуществляется без контроля за исполнением приказов. Команды исполнительному звену системы выдаются по заданной жесткой программе. Подобным образом построено управление станками-автоматами с программой, записанной на пер-

26

 

фокартах или магнитной ленте. Управление на основе только прямой связи в простых системах возможно благодаря – тому, что объекты управления в этих системах не подвержены действию возмущений. Если же эти возмущения, то система выходит из строя. Например, если в станке-автомате деталь выпадает из зажима, то процесс обработки прекращается.

В сложных динамических системах, подверженных

возмущениям, управление, как правило, происходит

при наличии обратной связи и контроля за процессом управления. Роль обратной связи между объектом уп­равления и управляющей частью выполняет какое-либо измерительное устройство и канал обратной связи. Из­мерительное устройство измеряет реальное значение регулируемой величины х и посылает эту информацию в управляющую часть. Информация о реальном значении регулируемой величины поступает в аппарат срав­нения, который производит сравнение реального значения регулируемой величины х с заданным, программ­ным значением f. Для этого аппарат сравнения дол­жен.обладать указанной программой f, по которой и осуществляется управление. Как указывалось выше, эта программа может быть как заложена в структуре са­мого аппарата сравнения, так и вводиться извне от более высших центров регуляции. На основе сравнения, которое мы обозначим как вычитание: f — х, ап­парат сравнения определяет рассогласование между программным и реальным значением регулируемой величины и информацию о величине рассогласования пе­редает в устройство управления. Устройство управле­ния на основе величины рассогласования вырабатывает соответствующий корректирующий сигнал управления, который передается на объект управления. Сигнал управления имеет такое информационное содержание, которое приводит к изменению процессов в объекте управления в сторону уменьшения рассогласования. Информация" о результате действия снова передается измерительным устройством в управляющую часть, ко­торая вновь производит коррекцию управления. Описанный процесс регулирования будет продолжаться до тех пор, пока рассогласование не станет равным нулю. Так как на систему постоянно действуют возмущения и в результате того, что любая система обладает инер­цией, процесс регулирования происходит постоянно.

27

 

 

 

При этом регулируемая величина совершает колебания около заданного значения (рис. 2).

Программа, по которой осуществляется управление, может быть статической — неизменной во времени и динамической — когда программное значение регулиру­емой величины является функцией времени (см. рис. 2).

Если программа вводится в аппарат сравнения выс­шим центром регуляции, то система регулирования мо­жет работать в любом режиме, задаваемом этим выс­шим центром.

Эффективность управления зависит от количественной характеристики, регулирующей системы во време­ни. Если на объект управления подействовало возму­щение, то регулируемая величина отклоняется от за данного значения —возникает начальное рассогласование. В процессе дальнейшего регулирования величина приближается к программному значению. Кривая, по которой регулируемая величина переходит от одного значения к другому, называется кривой переходного процесса или кривой процесса регулирования. Чем бы­стрее происходит согласование регулируемой величины с заданным значением, и чем ближе кривые регулиро­вания к заданной программной линий, тем лучше пара­метры регулятора,

Количественным показателем процесса регулирова­ния может быть площадь регулирования, которая пред­ставляет собой площадь замкнутой области, ограни­ченную с одной стороны линией программного значе­ния регулируемой величины, а с другой — кривой пере­ходного процесса. При этом чем меньше площадь ре-

28

 

гулирования, тем выше его качество. Данный метод оценки качества регулирующих систем может быть при­менен в физиологических и медицинских исследовани­ях. Различные функциональные пробы, которые приме­няются в физиологии и медицине, являются дозирован­ными возмущениями. Введение показателя — площади регулирования — позволит количественно оценить регу­лирующие системы организма, что будет способствовать повышению объективности медицинской диагностики. При этом за линию программного значения регулируе­мой величины может быть принята линия равновесного режима, получаемая в условиях отсутствия возмуще­ний.

Таким образом, любая система управления может быть охарактеризована тремя следующими особенностями: 

1) прямой связью между управляющей и управляемой частями системы, по которой поступают сигналы управления;

2) обратной связью управляемой и управляющей частей системы, которая позволяет контро­лировать процесс управления и производить его коррекцию;  

3 ) переработкой информации о текущем со стоянии управляемого объекта, поступающей по каналам обратной связи, в сигналы управления и осуществляемой при посредстве аппарата сравнения.

В организме все процессы являются регулируемыми и регуляция осуществляется на основе наличия обратной связи. В отличие от технических систем биологиче­ские обратные связи характеризуются нелинейностью, когда между выходной величиной и результатом коррекции нет прямой зависимости. Это способствует по­вышению точности регулирования. Так, если компенси­рующий эффект прямо пропорционален возмущению или рассогласованию, то за время, в течение которого происходит включение корректирующих механизмов, продолжающееся действие возмущения приводит к не. учитываемому отклонению регулируемой величины от первоначального значения. Поэтому последующая коррекция на основе ранее зафиксированного рассогласо­вания не дает желаемого эффекта. Как показано Гольдманом, особенность регулирующих систем организмов состоит в том, что регулирование в них осуществляется как по отклонению—рассогласованию, так и по его первой и второй производным, т. е. по скорости и ускорению рассогласования. Это обеспечивает большую точ-                                                                  29

 

ность регулирования и позволяет организму избегать

состояний, опасных ДЛЯ жизни.

0братная связь имеет большое значение в регулировании самых различных процессов в организме. П.К.. Анохин ещё в 1935 г. указал на важное значение обратной связи, названной им обратной афферентацией, для осуществления приспособительных реакций нервной системы. Если раньше в физиологии было по­нятие о рефлекторной дуге, то в настоящее время об­щепризнано наличие рефлекторного кольца. Рефлек­торная дуга замыкается обратной связью между эф­фекторами и центральной нервной системой.

Все произвольные движения человека осуществляются при наличии обратных связей. Это можно проде­монстрировать на самом простом примере. Допустим, человек выполняет целенаправленный двигательный акт, например, пытается взять со стола какой-нибудь предмет. При этом нервные импульсы от головного моз­га идут по соответствующим нервам к мышцам руки и вызывают ее движение. Это прямая связь, по которой поступают сигналы управления. Движение руки все время контролируется зрительным — и кинетическим анализаторами. Информация от этих двух рецепторов, осуществляющих обратную связь, поступает в мозг, где результат действия сличается с программой достиже­ния цели. На основе этого вырабатываются коррек­тирующие сигналы, и реальная траектория движения руки приближается к заданной (схема 2). Благодаря этой постоянной коррекции человек может совершать точные целенаправленные движения. В контролиро­вании движений принимают участие и другие анали­заторы.

  Регулирование процессов на основе обратных связей наблюдается не только на уровне целого организма, как в приведенном примере, но и на молекулярном, кле­точном и системном уровнях организации. Саморегуляция в некоторой степени присуща самим химическим реакциям. Свойство саморегуляции химических реакция, направленное на стабилизацию выхода продуктов реакции, отражено в принципе Ле-Шалелье:

если на химическую систему действуют возмущения,

 то процессы в системе перестраиваются так, чтобы компенсировать действие возмущения и стабилизировать

систему.       

³⁰     

 

 

 

Схема 2. Схема системы управления рукой при совершении целе­направленного движения.

Можно привести такой пример саморегуляции хи­мической реакции в организме. Известно, что универсальным источником энергии в клетках является энер­гия гидролиза АТФ. АТФ образуется за счет энергии гликолиза и окислительного фосфорилирования. Ока­зывается, что концентрация АТФ в клетках способна поддерживаться на постоянном уровне в большой сте­пени за счет собственного механизма саморегуляции. Если увеличивается распад АТФ (при возрастании ак­тивности клеток), то это приводит к увеличению кон­центрации АДФ и минерального фосфата. Повышение концентрации АДФ и фосфата, согласно закону дейст­вующих масс, стимулирует окислительное фосфорилирование, что приводит к увеличению выхода АТФ (схе­ма 3). При снижении скорости расщепления АТФ умень­шаются стационарные концентрации АДФ и фосфата, что приводит к снижению интенсивности фосфорилирования и к уменьшению выхода АТФ. В данном случае информация, которая используется для регулирования, передается через изменение стационарных концентраций реагирующих веществ. Данный вид регуляции может контролироваться другими механизмами, например, пу­тем изменения проницаемости мембран, которое будет вызывать изменение стационарных концентраций. Важно отметить, что кодирование внешней информации в виде набора стационарных концентраций происходит незави­симо от информации нуклеиновых кислот. По мнению некоторых ученых, механизмы биологической информа-

31

 

 

Схема 3. Схема саморегуляции реакций синтеза я распада АТФ.

ции, связанные со стационарными концентрациями и мембранами, являются более древними, чем механизмы, связанные с нуклеиновыми кислотами.

Очень важным свойством живых систем является поддержание гомеостаза, под которым понимается постоянство параметров внутренней среды организма. Основная идея гомеостаза состоит в том, что организм изменяет свои внутренние и внешние связи так, чтобы сохранить постоянство ряда существенных для него показателей внутренней среды.  Гомеостатическими величинами у млекопитающих являются температура тела, активная реакция и осмотическое давление крови, концентрация кислорода, глюкозы, ионов в крови и т. д.

Поддержание гомеостаза осуществляется в результа­те саморегуляции на основе обратной связи. Во всех

случаях роль управляющей части выполняют головной

мозг, где главное значение принадлежит гипоталамусу, и железы внутренней секреции. Управляемой частью являются внутренние органы и мышцы. Каналами прямой

 и обратной связи служат эфферентные и афферентные нервы и кровеносное русло, по которому передается гуморальное воздействие. Измерительнымустройством являются рецепторы: терморецепторы, хеморецепторы и пр. Гомеостатические механизмы поддерживают регулируемые величины на оптимальном уровне. При действии небольших возмущений (измене­нии внешних условий) регулируемые величины не изме­няют своих значений. При действии сильных возмуще­ний регулирующие механизмы переводят их на другой, более оптимальный уровень. При этом все уровни ле­жат в пределах физиологических норм отклонений. На­конец, при очень значительном изменении внешних условий регулирующие механизмы не способны поддер-

32

 

 

Рис. 3. Схема регулирования температуры тела (по Хэнзелу, 1966).

живать гомеостаз. Регулируемые величины выходят за пределы физиологических норм развивается патологическое состояние.

Работу гомеостатических систем регулирования можно проследить на примере работы системы регули­рования температуры тела у гомойотермных животных (рис. 3). Регулирование осуществляется центрами тер­морегуляции, локализованными в гипоталамусе. Регу­лирование происходит по динамической программе: ут­ром средняя температура тела человека 36,5 °С, вече­ром 37,5 °С; точность регулирования ±0,1 °С.

Температура тела поддерживается на определенном уровне благодаря тому, что скорость теплопродукции в организме равняется скорости теплоотдачи. Первичны­ми источниками тепла в организме являются процессы

3 Медицинская биофизика

33

 

окисления в мышцах (зависят от интенсивности мы­шечной деятельности) и во внутренних органах. При изменении интенсивности данных процессов изменяет­ся скорость теплопродукции. Скорость теплоотдачи из­меняется в результате следующих основных процессов: изменений интенсивности потоотделения, кровотока в коже, частоты дыхания, величины поверхности тела, положения волос. Если температура тела отклоняется от заданного значения, то информация об этом от терморецепторов, а также непосредственно с кровью, омывающей гипоталамус, поступает в центр регуляции. Центр терморегуляции на основе анализа этой инфор­мации вырабатывает соответствующие сигналы управ­ления и посылает их по двигательным и вегетативным нервам к органам, ответственным за теплопродукцию и теплоотдачу. В результате этого скорости теплопродукции и — теплоотдачи изменяются таким образом, что рассогласование устраняется. Точность регулирования температуры тела обусловлена тем, что терморецепто­ры кожи посылают в центр регуляции информацию о действии возмущений (изменении температуры внеш­ней среды) еще до того, как начинает изменяться температура тела. Кроме того, точность регулирования зависит и от условнорефлекторной деятельности, которая позволяет центру регуляции «предвидеть» действие возмущений и заранее выработать соответствующие сигналы управления.

Необходимым условием нормального функционирования гомеостатических механизмов являются сохранность и нормальная работа всех элементов замкнутого контура регулирования. Патологическое состояние может вызываться как нарушением работы элементов, относящихся к управляющей части и системе прямой связи так и нарушением работы элементов, относящихся к системе контроля и обратной связи. Механизмы обратной связи в организме в настоящее время изучены срав­нительно слабо. А между тем значение их имеет исклю­чительно большое значение в медицине.

Например, диабет не всегда вызывается нарушением функций поджелудочной железы, он может быть свя­зан также с патологией глюкорецепторов.

Все вышеописанные системы регулирования имеют отрицательную обратную связь. Можно отметить, что наличие отрицательной обратной связи всегда приво-    34

дит к устранению рассогласования в системе, к стабилизации системы. Имеется и другой вид обратной связи — положительная обратная связь. Примером системы с положи­тельной обратной связью может служить такое явле­ние: от симпатического отдела вегетативной нервной системы идут импульсы к надпочечникам (прямая связь). В кровь при этом выделяется адреналин. Ока­зывается, что, достигая мозга по кровеносному руслу, адреналин активизирует — нервную систему, что приво­дит к повышению частоты импульсов к надпочечникам и к более интенсивному выделению адреналина. Возра­стание активности продолжается до тех пор, пока клет­ки не достигнут некоторого предела своих возможно­стей. В данном случае адреналин осуществляет обрат­ную связь надпочечников с мозгом. При положительной обратной связи элементы системы объединяются в замкнутый контур, каждый элемент стимулирует последующий к изменению. За счет этого процессы в системах с положительной обратной связью развиваются с ускорением. При этомускорение может быть как в сторону усилениявыходного эффекта, так и в сторону его ослабления. Положительная обратная связь поддерживает

неравновесное состояние системы – рассогласова ние в данных системах с течением времениувеличивает­ся. Под рассогласованием нужно понимать не разность между реальным и заданным значениями регулируемой величины, как в случае отрицательной обратной связи, а разность между настоящим и последующим значени­ем регулируемой величины.

Положительная обратная связь встречается там, где за небольшой промежуток времени необходимо получить максимальное значение выходного эффекта, Втехнике она применяется для генерирования колебаний в раз­личных электронных схемах. Примером механизма с по­ложительной обратной связью в клетке является гене­рирование потенциала действия. При этом деполяриза­ция клеточной мембраны приводит к увеличению про­ницаемости мембраны для натрия. Увеличение прони­цаемости мембраны обусловливает более сильную диф­фузию натрия в цитоплазму и еще большее изменение мембранной разности потенциалов. За счет положитель-

3*                                                                                        35

 

ной обратной связи, потенциал действия достигает максимального значения за десятитысячные доли секунды.

Примером явления с положительной обратной связью может служить развитие некоторых патологических  процессов в организме. Вследствие действия какого-либо чрезмерного раздражителя происходит нару­шение деятельности какого-то одного органа. Наруше­ние деятельности этого органа выводит из равновесия следующий, а тот в свою очередь по обратным связям воздействует снова на первый, усугубляя его патологию (как это бывает при шоке).

Регулирование на уровне целостного организма. Живой организм представляет собой сложную саморе­гулирующуюся систему. Организм состоит из ряда бо­лее простых систем — физиологических систем. У выс­ших животных мы различаем нервную, сердечно-сосу­дистую, пищеварительную и другие системы. Физиоло­гические системы функционируют в тесной взаимосвязи друг с другом, обеспечивая целостные реакции всего организма. Деятельность живого организма как единой интегративной системы происходит благодаря тому, что в организме имеются специфические регулирующие си­стемы, осуществляющие взаимосвязь всех остальных си­стем организма. Длительный эволюционный процесс постепенного усложнения биологических систем путем надстройки все новых уровней регуляции привел к по­явлению организмов с многоуровневой и разнотипной регуляцией.

По Н. М. Амосову, существуют четыре типа регули­рующих систем. Первая система условно названа хими­ческой неспецифической системой. Она обеспечивает взаимодействие клеток и органов через продукты обме­на: продукты обмена одного органа воздействуют на другие органы и изменяют их деятельность. Продукты обмена — (метаболиты — не являются ни гормонами, ни медиаторами.

Вторая регулирующая система — эндокринная, или гормональная. Эндокринная система осуществляет ре­гуляцию деятельности различных органов путем выде­ления особых веществ — гормонов.

Третья регулирующая система представлена вегета­тивной нервной системой. С помощью нервной системы осуществляется дистанционное и оперативное управле­ние из одного центра одновременно несколькими объек-

36

 

тами. Основная функция вегетативной нервной систе­мы— поддержание гомеостаза.

Четвертая регулирующая система — это головной мозг и центральная нервная система. Головной мозг вы­полняет, с одной стороны, высшие функции по поддер­жанию гомеостаза, с другой — функцию уравновешива­ния целостного организма с внешней средой.

Для физиологии последних десяти лет характерен системный подход к изучению процессов в организме. Данное направление базируется не на представлении о физиологических системах, которое является более морфологическим, а на представлении о функциональных системах. Под функциональной системой, по П. К. Ано­хину, понимается совокупность разнородных органов и тканей, обеспечивающих выполнение определенной функции организма. Примером функциональной систе­мы является система регулирования температуры тела (см. рис. 3). В основе функциональной системы лежит система саморегуляции с отрицательной обратной связью, которая регулирует какую-либо величину. Бла­годаря наличию отрицательной обратной связи функция устойчива и стабильна к действию возмущений.

Представление о функциональных системах являет­ся более плодотворным при анализе целостных реакций организма, чем представление о физиологических си­стемах, так как оно позволяет лучше устанавливать связи между органами при выполнении функций. Б функциональную систему всегда входят элементы, от­носящиеся к различным физиологическим системам, и в обязательном порядке элементы двух основных регу­лирующих систем организма: нервной и эндокринной. По существу, функциональная система является едини­цей интегративной деятельности организма. Регулирую­щие механизмы функциональных систем обеспечивают адекватные ответы на различные воздействия. Общность всех этих ответов состоит в уравновешивании функцио­нальной системы целостного организма путем приведе­ния ее к стационарному режиму.

Особенность регулирующих механизмов, лежащих в основе функциональных систем, состоит в том, что уп­равляющие системы образуют несколько этажей и ре­гулирование осуществляется на нескольких уровнях. Например, постоянство концентрации глюкозы в крови может поддерживаться гомеостатическим механизмом

37

 

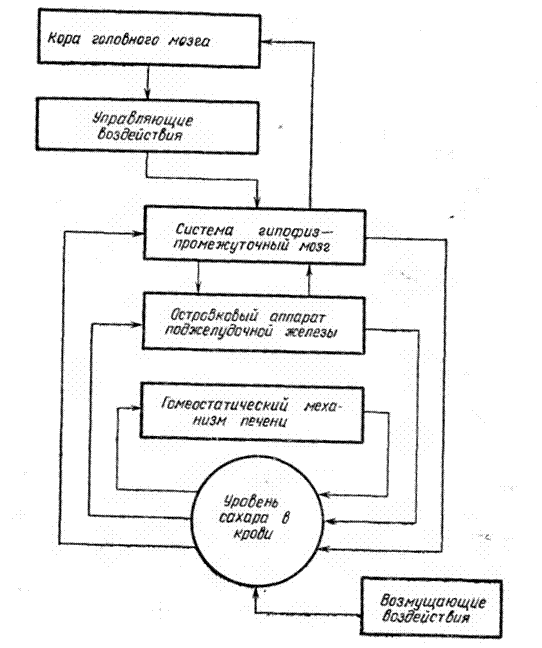Рис. 4. Общая схема регулирования уровня сахара в крови (по Дришелю, 1966).

печени. Вторым уровнем регулирования является гомеостатический механизм поджелудочной железы (рис. 4). Этот механизм без вмешательства мозга (гипофиза) с помощью гормонов инсулина и глюкагона регулирует содержание сахара в крови. Наконец, третий уровень представлен гипофизом и промежуточным мозгом, на-

38

 

ходящимися под контролем коры больших полушарий. Гипофиз и промежуточный мозг при помощи своих гор­монов способны как непосредственно, так и через под­желудочную железу изменять уровень сахара в крови. Взаимодействие низших и высших уровней сложной системы основано на обмене информацией по принци­пу обратной связи. Низшие уровни обладают известной автономностью. Пока поступающая информация не вы­ходит за определенные пределы, они способны само­стоятельно вырабатывать соответствующие целесооб­разные реакции. При этом на высший уровень не посы­лаются никакие сообщения, и высшие уровни могут не принимать участия в местных регуляторных процессах. Вмешательство высших уровней в работу низших про­исходит в том случае, когда последние не способны пе­рерабатывать весь поток информации при действии зна­чительных возмущений.

Глава 2