1. Какая связь называется функциональной?
2. Какая связь называется корреляционной?
3. Увеличивается или уменьшается величина результативного признака с увеличением факторного признака, в случае прямой связи?
4. Приведите формулу расчета коэффициента Фехнера.
5. Приведите формулу расчета коэффициента корреляции рангов Спирмена.
6. Какие показатели относятся к «тетрахорическим показателям».
7. Приведите формулу расчета коэффициента ассоциации Пирсона.
8. Приведите формулу расчета коэффициента коллигации Юла и Кендела.
9. Приведите формулу расчета коэффициента взаимной сопряженности Крамера и Чупрова.
10. Приведите формулу расчета величины интервала Стерджесса.
11. Если связь между признаками нелинейная, какой показатель характеризует силу связи при использовании метода аналитических группировок? Приведите формулу.
12. Если связь между признаками линейная, какой показатель характеризует силу связи при использовании метода аналитических группировок? Приведите формулу.
13. Сформулируйте правило сложения дисперсий.
14. Что служит показателем тесноты связи между признаками в аналитической группировке?
15. Приведите формулу расчета корреляционного отношения.
16. В каком интервале может принимать значение корреляционное отношение?
17. Приведите формулу расчета коэффициента детерминации.
18. В каком интервале может принимать значение коэффициент детерминации?
19. Что такое корреляция?
20. Что такое регрессия?
21. Какая корреляция, регрессия называется парной?
22. Какая корреляция, регрессия называется множественной?
23. Что такое линейная корреляция, регрессия? Какой функцией она выражена?
24. Что такое нелинейная корреляция, регрессия? Какой функцией она выражена?
25. Какие методы используют для определения вида функции в парной регрессии?
26. Какой вид имеет модель парной линейной регрессии?
27. Какой вид имеет модель множественной линейной регрессии?
28. Каким требованиям должен отвечать фактор в модели парной регрессии?
29. Приведите уравнение парной линейной регрессии.
30. Что такое случайная величина в модели парной линейной регрессии?
31. Какой метод позволяет минимизировать сумму квадратов отклонений фактических значений результативного признака от теоретических?
32. Приведите систему уравнений для расчета параметров парной линейной регрессии.
33. Приведите готовые уравнения для расчета параметров парной линейной регрессии.
34. Что такое свободный член уравнения? Каков его экономический смысл?
35. Что показывает коэффициент парной линейной регрессии?
36. Какой вид имеет корреляционная таблица, и для чего она используется?
37. Что показывает график «корреляционное поле»?
38. Приведите формулы расчета линейного коэффициента парной корреляции.
39. В каком интервале могут принимать значения линейного коэффициента парной корреляции?
40. Приведите формулу расчета линейного коэффициента парной детерминации, что он показывает?
41. Какой критерий позволяет определить существенность уравнения парной линейной регрессии?
42. Приведите формулу расчета фактического критерия Фишера (F-критерия) для парной линейной модели.
43. В каком случае уравнение парной линейной регрессии признается статистически значимым?
44. Какой критерий позволяет определить существенность параметров уравнения 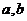 и коэффициента корреляции
и коэффициента корреляции  ?
?
45. Приведите формулы расчета критерия Стьюдента (t-критерия) для параметров уравнения 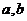 и коэффициента корреляции
и коэффициента корреляции  , в случае парной линейной модели.
, в случае парной линейной модели.
46. В каком случае параметры уравнения 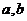 и коэффициент корреляции
и коэффициент корреляции  уравнения парной линейной регрессии признаются статистически значимыми?
уравнения парной линейной регрессии признаются статистически значимыми?
47. Какие функции относятся к нелинейным относительно включенного в модель фактора (независимой переменной), но линейным относительно результата (зависимой переменной)?
48. Какие функции относятся к нелинейным относительно включенного в модель результата, но линейным относительно фактора?
49. Что такое линеаризация нелинейных функций, ее цель?
50. Как проводится линеаризация полиномов разных степеней?
51. Как проводится линеаризация равносторонней гиперболы?
52. Как проводится линеаризация степенной функции?
53. Как проводится линеаризация показательной функции?
54. Что показывает коэффициент средней эластичности?
55. Приведите формулу расчета коэффициента средней эластичности для линейной функции.
56. Приведите формулу расчета коэффициента средней эластичности для функции параболы второго порядка.
57. Приведите формулу расчета коэффициента средней эластичности для функции равносторонней гиперболы.
58. Приведите формулу расчета коэффициента средней эластичности для степенной функции.
59. Приведите формулу расчета коэффициента средней эластичности для показательной функции.
60. Какой показатель характеризует силу связи в нелинейных моделях?
61. Приведите формулу расчета индекса корреляции для парной нелинейной модели.
62. В каком интервале может принимать значение индекс корреляции?
63. Что показывает индекс детерминации для парной нелинейной модели?
64. Приведите формулу расчета индекса детерминации для парной нелинейной модели.
65. Какой критерий позволяет определить существенность уравнения парной нелинейной регрессии?
66. Приведите общую формулу расчета фактического критерия Фишера для парной нелинейной модели?
67. Приведите формулу расчета фактического критерия Фишера для степенной  и показательной
и показательной  функций.
функций.
68. Приведите формулу расчета фактического критерия Фишера для второго порядка 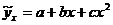 .
.
69. Приведите формулу расчета фактического критерия Фишера для параболы третьего порядка 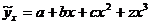 .
.
70. В каком случае уравнение парной нелинейной регрессии признается статистически значимым?
71. Что позволяет оценить средняя ошибка аппроксимации?
72. Приведите формулу расчета средней ошибки аппроксимации.
73. Чему равен допустимый предел средней ошибки аппроксимации?
74. Какой вид имеет доверительный интервал для уравнения регрессии  ?
?
75. Приведите формулу расчета стандартной ошибки для уравнения регрессии  .
.
76. Приведите формулу расчета доверительного интервала для уравнения регрессии  .
.
77. Какой вид имеет формула доверительного интервала для индивидуальных значений результативного признака  ?
?
78. Приведите формулу расчета стандартной ошибки для индивидуальных значений результативного признака  .
.
79. Приведите формулу расчета доверительного интервала для индивидуальных значений результативного признака  .
.
80. Какой вид имеет формула доверительного интервала для свободного члена уравнения регрессии  ?
?
81. Приведите формулу расчета стандартной ошибки для свободного члена уравнения регрессии  .
.
82. Приведите формулу расчета доверительного интервала для свободного члена уравнения регрессии  .
.
83. Какой вид имеет формула расчета доверительного интервала для коэффициента регрессии  ?
?
84. Приведите формулу расчета стандартной ошибки для коэффициента регрессии  .
.
85. Приведите формулу расчета доверительного интервала для коэффициента регрессии  .
.
86. Какие требования предъявляются к отбору факторов в модель множественной регрессии.
87. Что такое интеркорреляция?
88. Что такое мультиколлинеарность?
89. Приведите уравнение множественной линейной функции регрессии.
90. Приведите уравнение множественной степенной функции регрессии.
91. Приведите уравнение множественной показательной функции регрессии.
92. Приведите уравнение множественной функции регрессии экспоненты.
93. Приведите уравнение множественной функции регрессии гиперболы.
94. Приведите уравнение множественной функции регрессии параболы второго порядка.
95. Приведите систему уравнений, которую МНК дает для расчета параметров уравнения множественной линейной регрессии 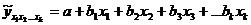 .
.
96. Как называется параметр  во множественной регрессии? Каков его экономический смысл?
во множественной регрессии? Каков его экономический смысл?
97. Приведите формулу расчета параметра  во множественной регрессии?
во множественной регрессии?
98. Что показывают коэффициенты регрессии  во множественной модели?
во множественной модели?
99. Что показывают стандартизованные коэффициенты регрессии  во множественной модели?
во множественной модели?
100. Приведите формулу расчета стандартизованных коэффициентов регрессии  для множественной линейной модели?
для множественной линейной модели?
101. Приведите систему уравнений, которую дает МНК для уравнения множественной регрессии в стандартизированном масштабе.
102. Что показывают частные уравнения регрессии?
103. Какой вид имеет система частных уравнений множественной регрессии для линейной функции.
104. Что показывают частные коэффициенты эластичности?
105. Что показывает средний коэффициент эластичности? Приведите формулу расчета.
106. Какой показатель характеризует тесноту связи во множественной модели?
107. Приведите формулу расчета показателя множественной корреляции.
108. Что показывает индекс множественной детерминации?
109. Приведите формулу расчета показателя множественной детерминации.
110. Приведите формулу расчета « » для нелинейных функций.
» для нелинейных функций.
111. Приведите формулу расчета скорректированного индекс множественной корреляции.
112. Что показывают коэффициенты частной корреляции?
113. Что такое коэффициенты частной корреляции нулевого порядка?
114. Что такое коэффициенты частной корреляции первого порядка?
115. Что такое коэффициенты частной корреляции второго порядка?
116. В каком интервале могут принимать значения коэффициенты частной корреляции?
117. Как рассчитываются частные коэффициенты корреляции через 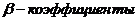 .
.
118. Что показывают частные коэффициенты частной детерминации? Приведите формулу расчета.
119. Какой критерий позволяет оценить значимость множественного уравнения регрессии?
120. Приведите формулу расчета критерия Фишера для множественной модели.
121. Какой критерий позволяет оценить значимость каждого отдельно включенного в модель фактора?
122. Приведите формулу расчета частного  , для фактора
, для фактора  .
.
123. Какой критерий позволяет оценить статистическую значимость параметров множественного уравнения регрессии?
124. Приведите формулу расчета критерия Стьюдента для множественной модели.
Тесты
| Тестовое задание | Ключ верного ответа | ||||
| Календарный модуль 1. Общая теория статистика | |||||
| Модульная единица 1.1. Предмет и метод статистики, статистика как общественная наука | |||||
| 1. Одним из значений термина «статистика» является: а) отрасль теоретической деятельности, которая не имеет целью сбор, обработку, анализ и публикацию массовых данных о различных явлениях общественной жизни, «статистический учет»; б)цифровой материал, который характеризует общественные явления или территориальные распределения какого-либо признака; в) отрасль математики. | б | ||||
| 2. Предметом статистики является: а) качественная сторона массовых общественных явлений в неразрывной связи с их количественной стороной; б) лишь качественная сторона массовых общественных явлений; в) лишь количественная сторона массовых общественных явлений. | а | ||||
| 3. Статистика относится: а) к гуманитарным наукам; б) к естественным наукам; в) статистика находится на стыке естественных и гуманитарных наук. | в | ||||
| 4. Статистическая совокупность – это: а) масса произвольно отобранных единиц; б) масса единиц объединенных единой качественной стороной; в) масса единиц полученных в результате произвольного статистического наблюдения. | б | ||||
| 5. Метод статистики включает методы: а) массовых наблюдений, группировок, обобщающих показателей. б) только метод группировок; в) только метод обобщающих показателей. | а | ||||
| 6. Статистический признак – это: а) количественная особенность единицы совокупности; б) качественная особенность единицы совокупности; в) количественная особенность статистической совокупности; | б | ||||
| 7. Статистический показатель – это: а) количественная особенность единицы совокупности; б) качественная особенность единицы совокупности; в) количественно-качественная обобщающая характеристика какого-то свойства группы единиц или совокупности в целом. | в | ||||
| Модульная единица 1.2. Статистическое наблюдение | |||||
| 8. Статистическое наблюдение – это: а) первый этап статистического анализа; б) второй этап статистического анализа; в) третий этап статистического анализа. | а | ||||
| 9. Статистическое наблюдение осуществляется в форме: а) подсчета корреспондентских агентов; б) предоставления плановой отчетности, или проведения специально организованного наблюдения; в) выявления статистических закономерностей. | б | ||||
| 10. Несплошное наблюдение: а) представляет собой сбор и получение информации обо всех единицах изучаемой совокупности; б) основано на принципе не случайного отбора единиц изучаемой совокупности, при этом в выборочной совокупности должны быть представлены все типы единиц, имеющихся в совокупности; в) основано на принципе случайного отбора единиц изучаемой совокупности, при этом в выборочной совокупности должны быть представлены все типы единиц, имеющихся в совокупности. | в | ||||
| 11. При экспедиционном виде опроса: а) регистраторы получают необходимую информацию от опрашиваемых лиц и сами фиксируют ее в формулярах; б) формуляры заполняются самими респондентами, регистраторы только раздают бланки и объясняют правила их заполнения; в) заключается в предоставлении сведений в соответствующие органы в явочном порядке. | а | ||||
| 12. Единицей наблюдения называют: а) первичный элемент объекта, который является непосредственным носителем признаков, подлежащих наблюдению; б) единица, от которой должны быть получены сведения в процессе наблюдения; в) объект осуществляющий наблюдение. | б | ||||
| 13. Система и способы наблюдений, система обработки данных, методы расчета всех показателей во всех звеньях общества должны быть подчинены требованиям: а) народно-хозяйственного целого для всей страны, всех звеньев; б) для каждой отрасли система и способы наблюдения разрабатываются отдельно; в) для каждой подотрасли система и способы наблюдения разрабатываются отдельно. | а | ||||
| Модульная единица 1.3. Обобщающие статистические показатели | |||||
| 14. Система статистических показателей - это: а) совокупность статистических единиц; б) свод основных правил статистики; в) это совокупность статистических показателей, отражающая взаимосвязи, которые объективно существуют между явлениями. | в | ||||
| 15. В однородной совокупности все признаки: а) имеют равное значение; б) имеют количественно равные значения; в) могут отличаться по величине изучаемого признака. | в | ||||
| 16. Производные показатели получают в результате: а) подсчета; б) расчета; в) подсчета или расчета. | б | ||||
| 17. Первичные показатели получают в результате: а) подсчета; б) расчета; в) подсчета или расчета. | а | ||||
| 18. Абсолютные статистические показатели измеряются: а) в натуральных единицах измерения; б) в относительных единицах измерения; в) не имеют единиц измерения. | а | ||||
| 19. Относительные статистические показатели: а) являются именованными величинами; б) не являются именованными величинами; в) не поддаются оценки. | б | ||||
| 20. Если в ходе расчета относительных статистических показателей величина, принятая за базу сравнения, приравнивается к единице, то форма относительной величины называться: а) коэффициент; б) темп; в) промилле. | а | ||||
| 21. Если в ходе расчета относительных статистических показателей величина, принятая за базу сравнения, приравнивается к 100, то форма относительной величины называться: а) коэффициент; б) темп; в) промилле. | б | ||||
| 22. Если в ходе расчета относительных статистических показателей величина, принятая за базу сравнения, приравнивается к 1000, то форма относительной величины называться: а) коэффициент; б) темп; в) промилле. | в | ||||
| 23. Если в ходе расчета относительных статистических показателей величина, принятая за базу сравнения, приравнивается к 10000, то форма относительной величины называться: а) коэффициент; б) темп; в) продецимилле. | в | ||||
| 24. Средние величины характеризуют: а) меру и степень вариации совокупности; б) центр распределения; в) форму (тип) распределения. | б | ||||
| Модульная единица 1.4. Сводка и группировка статистических данных. Статистические графики и таблицы | |||||
| 25. Статистическая сводка – это: а) первый этап статистического анализа; б) второй этап статистического анализа; в) трений этап статистического анализа. | б | ||||
| 26. Сводка называется простой, если: а) в ней отсутствуют группировки; б) в ней присутствуют только простые группировки; в) в ней присутствуют только сложные группировки. | а | ||||
| 27. Статистическая группировка – это: а) объединение в группы разнородных показателей; б) разбиение совокупности на группы, однородные по какому-то признаку; в) объединение в группы однородных и разнородных показателей. | б | ||||
| 28. Группировочный признак: а) признак, по которому происходит объединение двух и более совокупностей; б) признак, по которому происходит разделение совокупности на группы; в) признак, исключающийся из совокупности. | б | ||||
| 29. Группировочные интервал: а) промежуток между двумя крайними значениями группировочного признака, очерчивает границы групп; б) промежуток между двумя крайними значениями группировочного признака, очерчивает границы изучаемой совокупности; в) промежуток между двумя любыми значениями группировочного признака, не очерчивает границ групп и совокупности. | а | ||||
| 30. Группировочный интервалы бывают: а) только равные; б) только равные и открытые; в) открытые, закрытые, равные, неравные. | в | ||||
| 31. Величина интервала зависит от: а) только от вариации признака в изучаемой совокупности; б) только от количества единиц в изучаемой совокупности; в) как от вариации признака, так и от количества единиц в совокупности. | в | ||||
| 32. Группировка называется простой, если: а) все признаки, по которым она построена, не нуждаются в дополнительных расчетах; б) один из признаков, по которым она построена, не нуждается в дополнительных расчетах; в) она выполнена по одному признаку. | в | ||||
| 33. Иерархическая группировка: а) многомерная группировка, в которой значение последующего признака определяется областью значений предыдущего; б) многомерная группировка, в которой значение предыдущего признака определяется областью значений последующего; в) зависимости между признаками нет. | а | ||||
| 34. Типологическая группировка: а) расчленение совокупности на группы, характеризующие ее строение; б) разбиение исследуемой совокупности на социально-экономические классы; в) позволяет охарактеризовать взаимосвязи между изучаемыми признаками. | б | ||||
| 35. Структурная группировка: а) группировка, в которой происходит разделение однородной совокупности на группы, характеризующие ее структуру по какому-то варьирующему признаку; б) группировка, в которой происходит разделение однородной совокупности на группы, характеризующие ее структуру по какому-то не варьирующему признаку; в) позволяет охарактеризовать взаимосвязи между изучаемыми признаками. | а | ||||
| 36. Аналитическая группировка: а) расчленение совокупности на группы, характеризующие ее строение; б) разбиение исследуемой совокупности на социально-экономические классы; в) позволяет охарактеризовать взаимосвязи между изучаемыми признаками. | в | ||||
| 37. Статистические таблицы – это: а) Статистической называется таблица, которая содержит сводную числовую характеристику исследуемой совокупности по одному или нескольким существенным признакам, взаимосвязанным логикой экономического анализа; б) вспомогательные математико-вычислительные таблицы; в) справочные таблицы. | а | ||||
| 38. Сказуемое таблицы – это: а) это объект статистического изучения, то есть отдельные единицы совокупности, их группы или вся совокупность в целом; б) перечень граф и диаграмм таблицы; в) это статистические показатели, характеризующие изучаемый объект. | в | ||||
| 39. Подлежащее таблицы –это: а) это объект статистического изучения, то есть отдельные единицы совокупности, их группы или вся совокупность в целом; б) перечень граф и диаграмм таблицы; в) это статистические показатели, характеризующие изучаемый объект. | а | ||||
| 40. Статистические графики: а) условное обозначение числовых величин и их соотношений в виде графических (геометрических) образов – точек, линий, плоскостных фигур, их сочетаний и различного расположения; б) условное обозначение числовых величин и их соотношений в виде линий в) статистика пользуется специфическими методами изображения графиков. | а | ||||
| 41. Возрастающим графиком называется график, на котором: а) возрастанию значений на оси X соответствует возрастание значений на оси Y; б) возрастанию значений на оси Х соответствует убывание значений на оси Y; в) между значениями Х и значениями Y нет взаимосвязи. | а | ||||
| 42. Убывающим графиком называется график, на котором: а) возрастанию значений на оси X соответствует возрастание значений на оси Y; б) возрастанию значений на оси Х соответствует убывание значений на оси Y; в) между значениями Х и значениями Y нет взаимосвязи. | б | ||||
| 43. Ось абсцисс (Х): а) делит поле графика по диагонали; б) обычно вертикальная линия; в) обычно горизонтальная линия. | в | ||||
| 44. Ось ординат (Y): а) обычно горизонтальная линия; б) обычно вертикальная линия; в) делит поле графика по диагонали. | б | ||||
| Модульная единица 1.5. Средние величины и показатели вариации | |||||
| 45. Сущность средней заключается в том, что в ней: а) взаимопогашаются случайные отклонения значений признака но не учитываются изменения вызванные основным фактором; б) не взаимопогашаются случайные отклонения значений признака; в) взаимопогашаются случайные отклонения значений признака и учитываются изменения вызванные основным фактором. | в | ||||
| 46. Основные правила построения средних: а) необходимо не массовое обобщение фактов; б) качественная однородность совокупности; в) все единицы должны быть одинаковы. | б | ||||
| 47. Средняя не рассчитывается по: а) двум единицам; б) более чем по трем единицам; в) по всем выборочным совокупностям; | а | ||||
48. Общая формула расчета степенных средних имеет вид:
а) 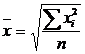 ;
б) ;
б)  ;
в) ;
в)  и и  ; ;
| в | ||||
| 49. Всего степенных средних можно рассчитать: а) от - ∞ до + ∞; б) от 0 до + ∞; в) от 0 до - ∞. | а | ||||
| 50. Вид степенной средней зависит от: а) количества единиц в совокупности; б) показателя степени; в) назначается произвольно. | б | ||||
| 51. Средние степенные простые применяют для расчета: а) сгруппированных данных; б) несгруппированных данных; в) атрибутивных показателей. | б | ||||
| 52. Средние степенные взвешенные применяют для расчета: а) сгруппированных данных; б) несгруппированных данных; в) атрибутивных показателей. | а | ||||
53. Формула средней арифметической имеет вид:
а)  и и  ;
б) ;
б) 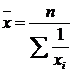 и и  ;
в) ;
в) 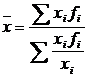 и и  . .
| а | ||||
| 54. Если к каждой варианте прибавить или отнять одно и то же постоянное число, то новая средняя: а) не изменится, так как число постоянно для всех вариант; б) увеличится или уменьшится на это же число; в) увеличится или уменьшится во столько же раз. | б | ||||
| 55. Если каждую варианту умножить или разделить на одно и то же постоянное число, то новая средняя: а) не изменится, так как число постоянно для всех вариант; б) увеличится или уменьшится на это же число; в) увеличится или уменьшится во столько же раз. | в | ||||
| 56. Сумма отклонений вариант от средней всегда: а) больше нуля; б) число отрицательное; в) всегда равна нулю. | в | ||||
| 57. Сумма квадратов отклонений вариант от средней всегда: а) меньше, чем сумма квадратов отклонений от любого другого числа; б) больше, чем сумма квадратов отклонений от любого другого числа; в) всегда равна нулю. | а | ||||
58. Формула средней гармонической имеет вид:
а)  и и 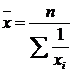 ;
б) ;
б) 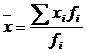 и и  ;
в) ;
в) 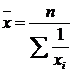 и и  . .
| в | ||||
59. Формула средней квадратической имеет вид:
а)  и и 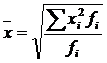 ;
б) ;
б)  и и  ;
в) ;
в) 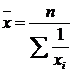 и и  . .
| а | ||||
| 60. Средняя геометрическая применяется для расчета: а) средних коэффициентов роста; б) средних коэффициентов прироста; в) средних уровней динамических рядов. | а | ||||
| 61. К структурным средним относится: а) мода, медиана, квартиль, дециль. б) средняя арифметическая и средняя квадратическая; в) дисперсия, и коэффициент вариации. | а | ||||
| 62. Модой называется: а) варианта признака, наиболее часто встречающаяся в исследуемой совокупности; б) значение изучаемого признака, которое занимает серединное место в ранжированном ряду единиц совокупности; в) значение изучаемого признака, которое занимает серединное место в произвольно расположенном ряду единиц совокупности. | а | ||||
| 63. Медианной называется: а) варианта признака, наиболее часто встречающаяся в исследуемой совокупности; б) значение изучаемого признака, которое занимает серединное место в ранжированном ряду единиц совокупности; в) значение изучаемого признака, которое занимает серединное место в произвольно расположенном ряду единиц совокупности. | б | ||||
| 64. Квартиль: а) делит ранжированный ряд на две части; б) на пять частей; в) на четыре части. | в | ||||
| 65. Дециль: а) делит ранжированный ряд на две части; б) на пять частей; в) на десять частей. | в | ||||
66. Для расчета моды в интервальном вариационном ряду применяют формулу:
а) 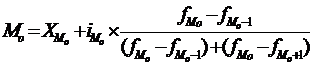 ;
б) ;
б)  ;
в) ;
в) 
| а | ||||
67. Для расчета медианны в интервальном вариационном ряду применяют формулу:
а) 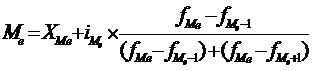 ;
б) ;
б)  ; ;
 . .
| б | ||||
| 68. Какой показатель указывает наличие вариации в совокупности: а) средняя арифметическая; б) мода; в) размах вариации. | в | ||||
69. Общая сумма квадратов отклонений вариант от средней рассчитывается как:
а) 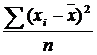 ;
б) ;
б)  ;
в) ;
в) 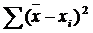 . .
| б | ||||
70. Дисперсия рассчитывается как:
а) 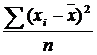 ;
б) ;
б) 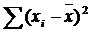 ;
в) ;
в) 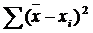 . .
| а | ||||
71. Среднее квадратическое отклонение рассчитывается как:
а) 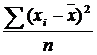 ;
б) ;
б) 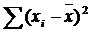 ;
в) ;
в)  . .
| в | ||||
| 72. Средний квадрат отклонений так же называется: а) стандартное отклонение; б) дисперсия; в) коэффициент вариации. | б | ||||
| 73. Среднее квадратическое отклонение измеряется в: а) в единицах измерения изучаемого признака; б) относительных единицах; в) в квадратах единиц измерения изучаемого признака натуральных единицах в квадрате. | а | ||||
| 74. Коэффициент вариации рассчитывается как: а) отношение среднего арифметического значения и среднего квадратического отклонения; б) отношение среднего квадратического отклонения и среднего арифметического значения; в) сумма стандартного отклонения и медианы. | б | ||||
| 75. Дисперсия постоянной величины: а) всегда число положительное; б) всегда число отрицательное; в) всегда равняется нулю. | в | ||||
| 76. Если все варианты увеличить или уменьшить на одну и ту же величину (А), то дисперсия: а) увеличится или уменьшиться на эту же величину; б) не изменится; в) увеличится или уменьшится во столько же раз. | б | ||||
| 77. Если все варианты умножить или разделить на одну и ту же величину (А), то дисперсия: а) увеличится или уменьшиться на эту же величину; б) не изменится; в) увеличится или уменьшится в А2 раз. | в | ||||
| 78. Дисперсия всегда меньше среднего квадрата отклонения вариантов от произвольной величины на: а) квадрат разности между средней арифметической и произвольной величиной; б) сумму отклонений вариант от средней; в) они равны. | а | ||||
| 79. Дисперсия алгебраической суммы независимых случайных величин равна: а) сумме стандартных отклонений; б) сумме квадратов отклонений; в) сумме их дисперсий. | в | ||||
80. Общая дисперсия рассчитывается как:
а) 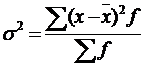 ;
б) ;
б) 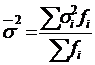 ;
в) ;
в) 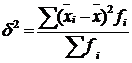 . .
| а | ||||
81. Внутригрупповая дисперсия рассчитывается как:
а)  ;
б) ;
б)  ;
в) ;
в) 
| б | ||||
82. Межгрупповая дисперсия рассчитывается как:
а)  ;
б) ;
б) 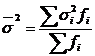 ;
в) ;
в)  . .
| в | ||||
83. Вариация альтернативного признака рассчитывается как:
а) 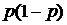 ;
б) ;
б)  ;
в) ;
в) 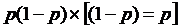 . .
| а | ||||
| 84. В нормальном распределении коэффициент распределения равен: а) единице; б) нулю; в) всегда положителен. | б | ||||
85. Коэффициент асимметрии рассчитывается как:
а)  ; где ; где 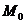 – мода;
б) – мода;
б)  где где 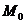 – мода;
в) – мода;
в)  где где  – медиана. – медиана.
| а | ||||
| 86. Показатель эксцесса характеризует: а) степень крутизны распределения; б) степень округлости распределения; в) полноту распределения. | а | ||||
| Модульная единица 1.6. Ряды динамики | |||||
| 87. Ряд динамики характеризует: а) изменение размеров явления во времени; б) распространение явления в пространстве; в) сравнение одной единицы совокупности с базовой величиной. | а | ||||
| 88. Параметры (показатели периодов времени) характеризующие ряд динамики – это: а) моменты времени или периоды, к которым относятся статистические данные; б) непосредственно статистические данные, характеризующие размер явления в определенный момент времени; в) расчетные формулы. | а | ||||
| 89. Уровнем ряда динамики называется: а) момент времени или период, к которым относятся статистические данные; б) непосредственно статистические данные, характеризующие размер явления в определенный момент времени; в) расчетные формулы. | б | ||||
| 90. Моментный динамический ряд – это: а) ряд, уровни которого отражают размеры изучаемого явления, за какой то промежуток времени; б) ряд, уровни которого выражают величину явления на определенный, конкретный момент времени; в) ряд, уровни которого отражают размеры территориально-моментно изучаемого явления. | б | ||||
| 91. Интервальный динамический ряд – это: а) ряд, уровни которого отражают размеры изучаемого явления за какой-то промежуток времени; б) ряд, уровни которого выражают величину явления на определенный, конкретный момент времени; в) ряд, уровни которого отражают размеры территориально-моментно изучаемого явления. | а | ||||
92. Начальный уровень динамического ряда, как правило, обозначается как:
а) только как 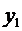 ;
б) только как ;
б) только как 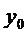 ;
в) как ;
в) как 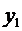 так и так и 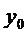 ; ;
| в | ||||
| 93. Текущим уровнем динамического ряда называют: а) сравниваемый уровень ряда динамики; б) уровень, по отношению к которому проводится сравнение; в) любой уровень статического ряда. | а | ||||
| 94. Базисным уровнем динамического ряда называют: а) сравниваемый уровень ряда динамики; б) уровень, по отношению к которому проводится сравнение; в) любой уровень статического ряда. | б | ||||
| 95. Базисным уровнем может быть: а) любой уровень, постоянно взятый за основу сравнения; б) уровень, предыдущий текущему уровню; в) только средний уровень. | а | ||||
| 96. Уровень динамического ряда можно разложить на; а) систематическую и постоянную компоненты; б) систематическую и случайную компоненты; в) ошибку и случайную компоненты. | б | ||||
| 97. Абсолютный прирост рассчитывается как: а) отношение двух уровней динамического ряда; б) разность двух уровней динамического ряда. в) произведение двух уровней динамического ряда; | б | ||||
| 98. Коэффициент роста рассчитывается как: а) отношение двух уровней динамического ряда; б) разность двух уровней динамического ряда; в) произведение двух уровней динамического ряда. | а | ||||
| 99. Коэффициент прироста рассчитывается как: а) разность абсолютного прироста к базисному уровню; б) коэффициент роста плюс 1; в) коэффициент роста минус 1. | в | ||||
| 100. Как темп роста (прироста) отличается от коэффициента роста (прироста): а) это одно и то же; б) темп – это коэффициент, умноженный на 100; в) темп – это коэффициент, плюс 100. | б | ||||
| 101. Абсолютное значение одного процента прироста показывает: а) часть абсолютного прироста, которая обеспечила 1% относительного прироста; б) часть относительного прироста, которая обеспечила 1% абсолютного прироста; в) сотая часть базисного уровня. | а | ||||
| 102. Абсолютное значение одного процента рассчитывается как: а) отношение двух уровней; б) разность двух уровней; в) как сотая часть предыдущего уровня. | в | ||||
| 103. Средний уровень интервального ряда динамики с равными интервалами рассчитывается как: а) средняя хронологическая; б) средняя арифметическая взвешенная; в) средняя арифметическая простая исходных уровней. | в | ||||
| 104. Средний абсолютный прирост рассчитывается как: а) средняя арифметическая из показателей абсолютного прироста; б) средняя арифметическая исходных уровней; в) отношение суммы абсолютных приростов к числу уровней динамического ряда. | а | ||||
| 105. Средний коэффициент (темп) роста рассчитывается по формуле: а) средней арифметической; б) средней геометрической; в) средней гармонической взвешенной. | б | ||||
| 106. Средний коэффициент (темп) прироста рассчитывается по формуле: а) средней арифметической; б средней гармонической взвешенной; в) как средний коэффициент (темп) роста минус 1 (100). | в | ||||
| 107. Тренд динамического ряда – это: а) наиболее часто встречающийся уровень динамического ряда; б) основная тенденция изучаемого динамического ряда; в) серединный уровень динамического ряда. | б | ||||
| 108. Для выявления тренда в динамических рядах используют: а) метод средних и метод серий; б) расчет моды и медианы; в) расчет показателей вариации. | а | ||||
| 109. К механическим методам выравнивания динамического ряда относится: а) метод укрупнения интервалов и метод скользящей средней; б) выравнивание по параболе второго порядка: в) выравнивание по прямой. | а | ||||
| 110. При выравнивании динамического ряда методом средних скользящих выбирают: а) только четное количество периодов; б) только нечетное количество периодов; в) как четное так и нечетное количество периодов. | в | ||||
| 111. К аналитическому выравниванию динамического ряда относится: а) метод укрупнения интервалов; б) метод скользящей средней; в) выравнивание по параболе второго порядка. | в | ||||
112. Оценку параметров уравнений  осуществляют используя:
а) метод наименьших квадратов (МНК);
б) метод наибольших квадратов (МБК);
в) метод усредненных квадратов (МСК). осуществляют используя:
а) метод наименьших квадратов (МНК);
б) метод наибольших квадратов (МБК);
в) метод усредненных квадратов (МСК).
| а | ||||
| 113. Оценку значимости уравнения выравнивания динамического ряда производят с помощью: а) критерия Стюарта; б) критерия Кокса; в) критерия Фишера. | в | ||||
114. При выравнивании динамического ряда по прямой МНК дает следующую систему уравнений:
а)  ;
б) ;
б)  ;
в) ;
в) 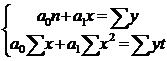 . .
| а | ||||
| 115. Экстраполяция в динамике предполагает: а) распространение полученных закономерностей на будущее время; б) определение значения недостающего недостающего ряда; в) распространение будущих выводов на прошлые периоды. | а | ||||
| 116. Интерполяция в динамике предполагает: а) распространение полученных закономерностей на будущее время; б) определение отсутствующего промежуточного уровня ряда; в) распространение будущих выводов на прошлые периоды. | б | ||||
| Модульная единица 1.7. Индексный метод в статистических исследованиях | |||||
| 117. В статистике под индексом понимается: а) абсолютный статистический показатель, который выражает соотношение величин какого-либо явления во времени, в пространстве, в сравнении фактических величин с эталоном; б) относительный статистический показатель, который выражает соотношение величин какого-либо явления во времени, в пространстве, в сравнении фактических величин с эталоном; в) произведение двух уровней динамического ряда. | б | ||||
| 118. Индивидуальные индексы служат для характеристики: а) изменения отдельных элементов сложного явления; б) сложного явления, составные части которого непосредственно несоизмеримы; в) сложного явления, составные части которого непосредственно соизмеримы. | а | ||||
| 119. Сводные (общие) индексы служат для характеристики: а) изменения отдельных элементов сложного явления; б) сложного явления, составные части которого непосредственно несоизмеримы; в) сложного явления, составные части которого непосредственно соизмеримы. | б | ||||
120. В международной практике количество (объем) принято обозначать:
а) 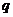 ;
б) ;
б)  ;
в) ;
в)  . .
| а | ||||
121. В международной практике себестоимость единицы продукции принято обозначать:
а) 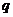 ;
б) ;
б)  ;
в) ;
в)  . .
| в | ||||
122. В международной практике цену единицы товара принято обозначать:
а) 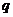 ;
б) ;
б)  ;
в) ;
в)  . .
| б | ||||
123. В международной практике выработку продукции в стоимостном выражении на одного рабочего или в единицу времени принято обозначать:
а) 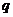 ;
б) ;
б)  ;
в) ;
в)  . .
| в | ||||
124. В международной практике выработку продукции в натуральном выражении на одного рабочего или в единицу времени принято обозначать:
а) 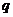 ;
б) ;
б)  ;
в) ;
в) 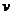 . .
| в | ||||
125. В международной практике общие затраты времени или численность рабочих принято обозначать:
а)   ;
б) ;
б)  ;
в) ;
в)  . .
| а | ||||
126. В международной практике стоимость продукции или товарооборот принято обозначать:
а) 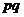 ;
б) ;
б)  ;
в) ;
в)  . .
| а | ||||
127. В международной практике издержки производства принято обозначать:
а) 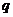 ;
б) ;
б)  ;
в) ;
в)  . .
| б | ||||
128. Используя международную практику обозначения индексируемых показателей, индекс физического объема продукции рассчитывается:
а)  ;
б) ;
б) 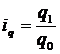 ;
в) ;
в)  . .
| б | ||||
129. Используя международную практику обозначения индексируемых показателей, индивидуальный индекс цен продукции рассчитывается:
а)  ;
б) ;
б)  ;
в) ;
в)  . .
| а | ||||
130. Используя международную практику обозначения индексируемых показателей, индивидуальный индекс себестоимости единицы продукции рассчитывается:
а)  ;
б) ;
б)  ;
в) ;
в) 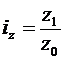 . .
| в | ||||
131. Используя международную практику обозначения индексируемых показателей, индекс количества продукции, произведенной в единицу времени, рассчитывается:
а)  ;
б) ;
б)  ;
в) ;
в) 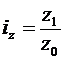 . .
| а | ||||
132. Используя международную практику обозначения индексируемых показателей, индекс производительности труда по трудовым затратам рассчитывается:
а)  ;
б) ;
б)  ;
в) ;
в) 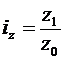 . .
| б | ||||
133. Используя международную практику обозначения индексируемых показателей, индивидуальный индекс выработки продукции в стоимостном выражении на одного рабочего рассчитывается:
а)  ;
б) ;
б)  ;
в) ;
в) 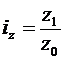 . .
| а | ||||
| 134. Числитель и знаменатель агрегатного индекса состоит из: а) произведения двух индексируемых величин; б) сумм двух индексируемых величин; в) произведения индексируемой величины и веса индекса. | в | ||||
| 135. Индексируемая величина в числителе и знаменателе индекса: а) остается неизменной; б) изменяется; в) не меняется в зависимости от величины индексируемой величины. | б | ||||
| 136. Вес индекса в числителе и знаменателе индекса постоянного состава: а) остается неизменной; б) изменяется; в) меняется в зависимости от величины индексируемой величины. | а | ||||
137. Агрегатный индекс стоимости продукции (товарооборота)  рассчитывается:
а) рассчитывается:
а)  ;
б) ;
б) 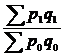 ;
в) ;
в) 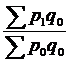 . .
| б | ||||
138. Агрегатный индекс физического объема продукции  рассчитывается:
а) рассчитывается:
а) 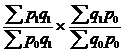 ;
б) ;
б) 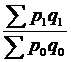 ;
в) ;
в) 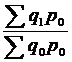 . .
| в | ||||
139. Агрегатный индекс цен  рассчитывается:
а) рассчитывается:
а) 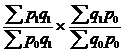 ;
б) ;
б) 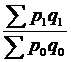 ;
в) ;
в)  . .
| в | ||||
140. К индексам переменного состава относится:
а) 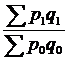 ;
б) ;
б)  ;
в) ;
в) 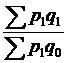 . .
| а | ||||
141. К индексам постоянного состава относится:
а) 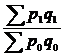 ;
б) ;
б)  ;
в) ;
в) 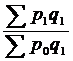 . .
| в | ||||
| 142. Средний индекс – это: а) индекс, вычисленный как средняя величина из агрегатных индексов; б) индекс, вычисленный как средняя величина из индивидуальных индексов; в) зависит от величины индексируемой величины. | б | ||||
143. Средний индекс физического объема:
а)  ;
б) ;
б)  ;
в) ;
в)  . .
| б | ||||
144. Средний индекс производительности труда:
а) 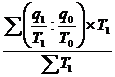 ;
б) ;
б)  ;
в) ;
в)  в. в.
| а | ||||
145. Средний индекс цен:
а)  ;
б) ;
б) 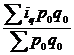 ;
в) ;
в) 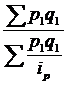 . .
| в | ||||
146. Средний индекс себестоимости:
а)  ;
б) ;
б) 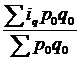 ;
в) ;
в)  . .
| в | ||||
| 147. Системой индексов называется: а) любой ряд последовательно построенных индексов; б) только ряд последовательно вычисленных индексов одного и того же явления с постоянной базой сравнения; в) только ряд последовательно вычисленных индексов одного и того же явления с меняющейся от индекса к индексу базой сравнения. | а | ||||
| 148. Системой цепных индексов называется: а) любой ряд последовательно построенных индексов; б) только ряд последовательно вычисленных индексов одного и того же явления с постоянной базой сравнения; в) только ряд последовательно вычисленных индексов одного и того же явления с меняющейся от индекса к индексу базой сравнения. | в | ||||
| 149. Системой базисных индексов называется: а) любой ряд последовательно построенных индексов; б) только ряд последовательно вычисленных индексов одного и того же явления с постоянной базой сравнения; в) только ряд последовательно вычисленных индексов одного и того же явления с меняющейся от индекса к индексу базой сравнения. | б | ||||
150. Между индексом издержек производства 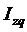 с индексами себестоимости с индексами себестоимости 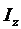 и физического объема и физического объема  продукции существует следующая взаимосвязь:
а) продукции существует следующая взаимосвязь:
а)  ;
б) ;
б)  ;
в) ;
в)  . .
| б | ||||
151. Между индексом затрат времени на производство продукции 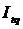 с индексами физического объема продукции с индексами физического объема продукции  и индексом трудоемкости и индексом трудоемкости  существует следующая взаимосвязь:
а) существует следующая взаимосвязь:
а) 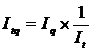 ;
б) ;
б) 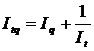 ;
в) ;
в) 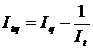 . .
| а | ||||
152. Индекс физического объема продукции равен:
а)  ;
б) ;
б)  ;
в) ;
в) 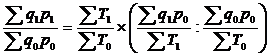 . .
| б | ||||
| 153. Дефлятор – это: а) коэффициент, переводящий значения стоимостного показателя за отчетный период в стоимостные измерители базисного; б) коэффициент, переводящий значения стоимостного показателя за отчетный период в натуральные измерители; в) коэффициент, переводящий значения стоимостного показателя за отчетный период в сопоставимые измерители. | а | ||||
| 154. Индекс-дефлятор рассчитывается как отношение фактической стоимости продукции отчетного периода к стоимости объема продукции: а) структура которого аналогична структуре отчетного года, но определенного в ценах базисного года; б) структура которого аналогична структуре отчетного года, определенного в ценах отчетного года; в) структура которого аналогична структуре базисного года, но определенного в ценах отчетного года. | а | ||||
| 155. В основе индекса-дефлятора лежит: а) формула Пааше; б) формула Ласпейреса; в) формула Струмилина. | а | ||||
| Модульная единица 1.8. Выборочный метод. Дисперсионный анализ | |||||
| 156. Выборочная совокупность – это: а) часть единиц генеральной совокупности подлежащих наблюдению; б) часть единиц генеральной совокупности не подлежащих наблюдению; в) все единицы изучаемой совокупности. | а | ||||
| 157. Генеральная совокупность – это: а) часть единиц генеральной совокупности подлежащих наблюдению; б) часть единиц генеральной совокупности не подлежащих наблюдению; в) все единицы изучаемой совокупности. | в | ||||
| 158. Расхождение между выборочной характеристикой и предполагаемой характеристикой генеральной совокупности: а) ошибка репрезентативности; б) ошибка генеральной совокупности; в) ошибка наблюдения. | а | ||||
| 159. Какой способ отбора не дает возможность один раз отобранной единице попасть в выборку еще раз: а) повторный; б) бесповторный; в) метод серий. | б | ||||
| 160. Какой способ отбора дает возможность один раз отобранной единице попасть в выборку еще раз: а) повторный; б) бесповторный; в) метод серий. | а | ||||
161. При механическом способе отбора единиц в выборку:
а) отбирается каждая пятая или каждая десятая или каждая сотая и т.д. единицы;
б) генеральная совокуп
Дата добавления: 2018-10-14; Мы поможем в написании ваших работ!; просмотров: 234 | Нарушение авторских прав Поиск на сайте: Лучшие изречения: |
Ген: 0.016 с.






